1 Lois de Kepler lois de Newton
Les lois de Kepler démontrées avril 2014. 2 Deuxième loi de Kepler : la loi des aires. On considère un corps céleste P de masse m soumis à l'attraction d'un
Démonstration des lois de Kepler à laide du calcul différentiel et
Première loi : Les planètes décrivent des orbites ellip- tiques dont l'un des foyers est le Soleil. Deuxième loi : La droite joignant le centre du Soleil au
Chapitre 5 : Application - Forces Centrales
La trajectoire des centres des planètes décrit une ellipse dont l'un des foyers est le soleil. Deuxième loi de Kepler. Les rayons vecteurs balaient des aires
∫ ∫ ∫
Les trois lois de Kepler. Mécanique 3 & 4ème - 4. La loi des aires. C'est la deuxième loi de Kepler. Le vecteur r. G balaie des aires égales pendant des
Chapitre 13 Mouvements des satellites et des planètes
Une ellipse dont les foyers sont confondus est un cercle de rayon R = a. Deuxième loi de Kepler ou loi des aires. Le segment [SP] qui relie le centre S du
PHQ114: Mecanique I
30/05/2018 La démonstration de ce fait capital repose sur la troisième loi de Newton ... deuxième loi de Kepler dite loi des aires : l'aire balayée par ...
Chapitre 17 Forces centrales
b Deuxième loi de Kepler (loi des aires). Dans le référentiel héliocentrique 3.6 Trajectoire conique (démonstration hors programme). Partons du PFD projeté ...
1 Les lois de Kepler : rappels ! a3 T2 = cste. 2 Construction de lorbite
• Deuxième loi : Le rayon Soleil-Planète balaie des aires égales pendant des Pour leur démonstration voir le fichier Kepler-démontré.pdf. P est une ...
Chapitre 12 : Mouvement des planètes et des satellites
géostationnaire. (10). Retrouver la troisième loi de Kepler pour un satellite ou une planète en mouvement circulaire uniforme.
Article Les fonctions trigonométriques et la deuxième loi de Kepler
Lemme 1 (bien connu des physiciens) Une courbe paramétrée z(t) satisfait la loi des aires si et seulement si elle est associée à une loi centrale. Démonstration
1 Lois de Kepler lois de Newton
Les lois de Kepler démontrées avril 2014. 2 Deuxième loi de Kepler : la loi des aires. On considère un corps céleste P de masse m soumis à l'attraction d'un
Démonstration des lois de Kepler à laide du calcul différentiel et
Première loi : Les planètes décrivent des orbites ellip- tiques dont l'un des foyers est le Soleil. Deuxième loi : La droite joignant le centre du Soleil au
Lois de KEPLER
La 2ème loi de Kepler implique que ces surfaces Une démonstration semblable est dans le livre avec au centre la Terre et un satellite en orbite…
? ? ?
yc. Page 8. Annexe II. Les trois lois de Kepler. Mécanique 3 & 4ème - 8. Autre démonstration de la première loi de Kepler vitesse et hodographe. Voici une
Rappels La démonstration des lois de Kepler repose dune part sur
La démonstration des lois de Kepler repose d'une part sur la 2 eme loi du mouvement de. Newton qui régit la trajectoire d'un corps de masse m en fonction de
Rappels La démonstration des lois de Kepler repose dune part sur
La démonstration des lois de Kepler repose d'une part sur la 2 eme loi du mouvement de. Newton qui régit la trajectoire d'un corps de masse m en fonction de
M ` ?
Première loi de Kepler. Les planètes décrivent des ellipses dont le Soleil est l'un des foyers. Deuxième loi de Kepler. Le rayon-vecteur (c.
Clemenceau
Les 3 lois de Kepler (Noblet). Chute d'un obus 2ème formule de Binet (pour l'accélération) : ... Démonstration de la 3ème loi de Kepler :.
Chapitre 5 : Application - Forces Centrales
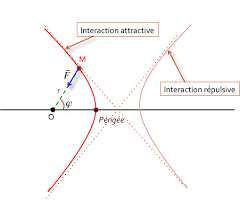
Loi des aires (2ème loi de Kepler):. La loi des aires stipule que la vitesse aréolaire est constante pour un mouvement à force centrale.
Chapitre 12 : Mouvement des planètes et des satellites
appliquant la deuxième loi de Newton aux satellites ou aux planètes. Retrouver la troisième loi de Kepler pour un satellite ou une planète en mouvement ...
Rappels
La dÿmonstration des lois de Kepler repose dþune part sur la 2emeloi du mouvement de Newton qui rÿgit la trajectoire dþun corps de masse m en fonction de la force Frqui lui est appliquÿ et qui sþexprime dans un rÿfÿrentiel galilÿen selon lþÿquation : amFrrI= [1] où arest le vecteur accélération.Pour mémoire, on rappelle que le vecteur vitesse est la dérivée première par rapport au temps
du vecteur position et le vecteur accélération est la dérivée seconde par rapport au temps du
vecteur position.Elle repose dþautre part sur le modýle de la loi de la gravitation universelle appliquÿe ü des
corps sphÿriques. Le thÿorýme du potentiel central stipule que la force dþattraction gravitationnelle exercÿe par un corps M de masse m prÿsentant une symÿtrie sphÿrique estidentique ü celle qui serait exercÿe si la totalitÿ de la masse m ÿtait concentrÿe en son centre.
La force quÿun corps sphþrique M1de masse m1exerce sur un autre corps sphériqueM2de masse m2sÿapplique conformþment ý la figure 1 et sÿþcrit : 2121
2 21
21
21MM
MM MM mmGFIII-=r r [2þ] où G est la constante de gravitation universelle.
Rþciproquement, la force dÿattraction gravitationnelle exercþe par le corps M2sur le corps M1
sÿþcrit : 12 12 2 12 12 12MM MM MM mmGFIII-=r r [2þþ] Figure 1 : Force dþattraction gravitationnelle FrConiques
On appelle conique tout ensemble de points M de coordonnées (x,y) dans un repère orthonormé (O,ir,jr)vérifiant une relation de la forme :02222=+II+II+I+IDyDxCyBxA
où A, B, C, D et E sont des nombres réels tels que A et B non tous deux nuls.Le tableau suivant donne les équations décrivant les coniques non dégénérées dans les repères
cartésien et polaire,et sous forme paramétrique :Type de conique Coordonnées
cartésiennesCoordonnées polaires Equation
paramétriqueCercle de rayon r
excentricité e=0 12 2 2 2 =+r y r x r=r q q sin cos I= I= ry rxEllipse de demi-grand
axe a et demi-petit axe b excentricité 0Parabole
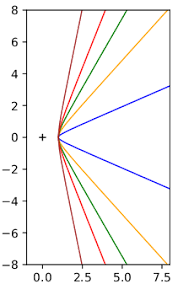
excentricité e=1 facteur dþÿchelle p xpyI=22 qrcos1I-=e p ty p tx =2 2Hyperbole
excentricité e>1 a bae 22+=12 2 2 2 =-b y a x qrcos1 2 I-=e ab q q tg by ax =cos
Le problème des 2 corps
En considérant le système à 2 corps décrit figure 1, la relation fondamentale de la dynamique
appliquée dans unrÿfÿrentiel galilÿen de centre O dÿfini arbitrairement sþÿcrit respectivement
ý partir de [2ÿ] et [2ÿÿ] pour chacun des corps M1et M2 : 12 12 2 12 12 2 1 2 1MM MM MM mmGdtOMdmIII-=I [3þ]
2121
2 21
21
2 2 2 2MM MM MM mmGdt
OMdmIII-=I [3þþ]
La somme de [3ÿ] et [3ÿÿ] donne immþdiatement : 02 2 2 221 2
1=I+Idt
OMdmdt
OMdm [4]
que lÿon peut rþþcrire sous la forme : ()02 22112 =I+I dt
OMmOMmd [5]
et dont une solution particulièrement évidente est :02211=I+IOMmOMm [6]
traduisant ainsi le fait que O est le centre de masse C (barycentre des masses ou centredþinertie) du systýme ü 2 corps et que le repýre orthonormÿ (C,ir,jr) constitue un repère
galiléen.Il vient alors facilement :
1 2 2121CMm
mmMMI+-= [7þ] 2 1 21
21CMm
mmMMI+= [7þþ] Les formules [3ÿ] et [3ÿÿ] sÿþcrivent alors respectivement : ()3quotesdbs_dbs2.pdfusesText_2
[PDF] 2m maroc 1990
[PDF] 2m maroc programme
[PDF] 2m site
[PDF] 2nd year maths chapter 2 exercise 2.2
[PDF] 3 4 equivalent in cooking
[PDF] 3 as bac
[PDF] 3 commerce private colege in bbsr
[PDF] 3 commerce syllabus
[PDF] 3 ejemplos de indice
[PDF] 3 eme svt genetique
[PDF] 3 exemple qui illustre la puissance mondiale des etat unis
[PDF] 3 membranes de l'oeil
[PDF] 3*500 bac 2015
[PDF] 3*500 bac bareme 2017
