[PDF] M ` ? Première loi de Kepler.

View - Download M ` ?

Previous PDF

Next PDF

Chapitre VII

Mouvements`a force centrale

VII.a. Lois de Kepler

En première approximation, le mouvement des planètes (1)autour du Soleil est régi par trois lois qui furent établies au 17 esiècle par l"astronome Johannes Kepler, à partir notamment des observations de

Mars réalisées par Tycho Brahe. Ces lois furent utilisées par Newton pour établir la loi de l"attraction

universelle. Voici leur énoncé traditionnel :Première loi de Kepler

Les planètes décrivent des ellipses dont le Soleil est l"un des foyers.Deuxième loi de Kepler

Le rayon-vecteur (c

.-à-d.le segment) Soleil-planète balaie des aires égales en des temps égaux.Troisième loi de Kepler

Le rapport du cube du demi-grand axe de l"ellipse sur le carré de la période de révolution autour

du Soleil est le même pour toutes les planètes.Nous démontrerons ces lois et préciserons leur signification et leurs limites dans ce qui suit.

VII.b. Mobile fictif

SoientR=(O;~{;~|;~k) un référentiel galiléen etM1etM2deux points matériels de massesm1etm2.

NotonsGle centre d"inertie du systèmeS=fM1;M2g: m

1!GM1+m2!GM2=~0:

On suppose queSest unsystème isolé. On a donc (m1+m2)~aG=R=P~Fext!S=~0, c.-à-d.~vG=R=~cte:

leréférentiel barycentriqueR=(G;~{;~|;~k) deSest donc galiléen.On se place désormais dansR.Z

On définit lemobile fictifMpar!GMB!M1M2B~r1. Rappelons que, par ordre croissant de distance au Soleil, les planètes du Système solaire sont Mercure, Vénus, la Terre,

Mars, Jupiter, Saturne, Uranus et Neptune. Elles eectuent leurs révolutions autour du Soleil quasiment dans le même

plan que la Terre. Ce dernier, appelé écliptique, est incliné d"environ 23 par rapport à l"équateur terrestre. 75
Michel FiocDynamique des systèmeset on lui associe lamasse réduite

Bm1m2m

1+m2:

Connaissant la position du mobile fictif, il est facile d"en déduire celles deM1etM2. En eet,!GM1=!GM2+!M2M1=m1!GM1=m2~r, donc

GM1=m2m

1+m2~r:

De même,

!GM2=m1m

1+m2~r:

En particulier, sim2m1(p.ex.la masse d"un satellite devant celle de la Terre ou la masse d"une planète devant celle du Soleil),!GM1~0 et!GM2~r:M1est alors presque confondu avecG, etM2avec M.Z

La trajectoire deMest déterminée par

F1!2=m2d2!GM2dt2=d2~rdt2:

On a

LG(fM1;M2g)=m1!GM1d!GM1dt+m2!GM2d!GM2dt

=m1!GM1d!GM1dt+m2!GM2d(!GM1+!M1M2)dt =(m1!GM1+m2!GM2| {z }

0)d!GM1dt+m2!GM2| {z }

~rd!M1M2dt; soit

LG(fM1;M2g)=~rd~rdtB~LG(M):

De même,

E c(fM1;M2g)=12 d~rdt 2

BEc(M):

VII.c. Constantes du mouvement

VII.c.1. Moment cinétique. 2eloi de Kepler

Le système étant isolé,

~LG=~cte. Notons~uzun vecteur unitaire colinéaire à~LGetL0=~LG~uz.

Le vecteur

~rétant perpendiculaire à~LG, donc à un vecteur~uzconstant,M se déplace dans le plan perpendiculaire à ~LGpassant par G. Soient~uxet~uydeux vecteurs tels que le repère (G;~ux;~uy;~uz) soit orthonormé direct. RepéronsMpar ses coordonnées polaires,r=k!GMket=(~uxb;!GM). On a

LG(M)=~rd~rdt=(r~ur)(:r~ur+r:~u)=r2:~uz:

La constante

CBr2:=L0=

s"appelle laconstante des aires(2).2. Certains auteurs appellent "constante des aires» la quantitéC=2.

76

Chapitre VII. Mouvements à force centrale

Pendant une durée infinitésimale dt, l"aire balayée par lerayon-vecteur!GMvaut (cf.§ I.a.1 pour

le calcul de l"aire d"un triangle) dA=k~rd~rk2 =jCj2 dt:

C"est ce qu"exprime laloi des aires, ou2eloi de Kepler: "Le rayon-vecteur balaie des aires égales en

des temps égaux.».L"aireA1balayée par!GMentre t

1ett1+test égale à l"aireA2

balayée entret2ett2+ t.

Cas oùm1m2

Sim1m2,~LM1(M2)=~LG(M), donc~LM1(M2)=~cte.

On peut démontrer ceci sans passer par le mobile fictif. Sim1m2,M1est confondu avecGet est

donc immobile dansR. En appliquant le théorème du moment cinétique àM2seul et en calculant

les moments par rapport àM1, on obtient d~LM1(M2)=dt=!M1M2~F1!2=~0, puisque~F1!2est une force centrale. VII.c.2. Énergie mécanique. Énergie potentielle eective M

1etM2interagissent par l"intermédaire d"uneforce centrale, c.-à-d.une force dirigée selon!M1M2

et ne dépendant que der=k!M1M2k. Une telle force est nécessairement conservative. Le système étant

isolé, son énergie mécanique,Em=Ec+Ep, est donc constante; notons-laE0. On a E 0=12 (:r2+r2:2)+Ep(r)=12 :r2+r2Cr 2 2! +Ep(r)=12 :r2+Eep(r); où E ep(r)BC22r2+Ep(r) est l"énergie potentielle eective.Z

On peut séparer les variablestetrdans l"équation diérentielle (enret:r) ci-dessus. On obtient

dt=drq

2 (E0Eep[r])=;

que l"on peut intégrer pour trouverten fonction der.

On a de même

d=Cdrr

2q2 (E0Eep[r])=:

77
Michel FiocDynamique des systèmesCas d"une force en 1=r2

Considérons le cas d"une force en 1=r2,

F1!2=Kr

2~ur:

K=Gm1m2correspond à la force gravitationnelle etK=q1q2=(4 0) à la force électrostatique.~F1!2

dérive alors de l"énergie potentielle d"interaction E p=Kr et E ep=C22r2Kr On a :r2=2 (E0Eep)=. Les seules valeurs derpossibles sont donc celles pour lesquellesEep(r)6E0.

Distinguons les cas suivants :

1.K>0.

On a lim

r!0Eep= +1et limr!1Eep=0. La fonctionEepa un minimum négatif unique en r

0=C2=K.

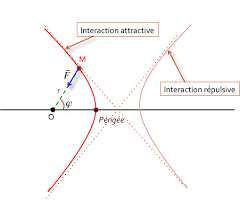
a.E0>0. L"équationE0Eep(r)=0 n"a qu"une seule racine,rmin. On a alorsr>rmin: la trajectoire s"étend jusqu"à l"infini. b.E0<0. L"équationE0Eep(r)=0 a deux racines,rminetrmax(rmax>rmin). On a alorsrmin6 r6rmax: la distance entreM1etM2est bornée.

2.K<0.

On a lim

r!0Eep= +1et limr!1Eep=0+. La fonctionEepest strictement décroissante. Comme dans le cas 1.a,E0>0 et l"équationE0Eep(r)=0 n"a qu"une seule racine,rmin. On a alorsr>rmin: la trajectoire s"étend jusqu"à l"infini.78

Chapitre VII. Mouvements à force centrale

Les pointsPetAcorrespondant àr=rminetr=rmaxs"appellent respectivement le péricentre et

l"apocentre. Dans le cas particulier d"un corps tournant autour de la Terre, on parle plutôt de périgée

et d"apogée; autour du Soleil, de périhélie et d"aphélie; autour d"une autre étoile, enfin, de périastre

et d"apoastre.

VII.d. Coniques

VII.d.1. Généralités

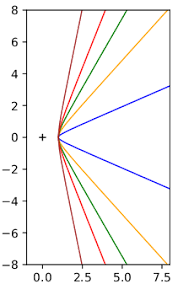
Considérons un cercleCet un pointSsitué hors du plan deC, sur la droite passant par le centre deCperpendiculaire au plan deC. L"ensemble des droites passant parSet s"appuyant surCforme un cône,K, de sommetS. Les coniques sont les courbes correspondant à l"intersection d"un planPavecK: ˆSiPest peu incliné par rapport au plan deC, on obtient une courbe fermée, l"ellipse. Le cercle est un cas particulier d"ellipse obtenu siPest parallèle àC.

ˆInclinonsunpeuplusP. Àuncertainmoment,Pdevientparallèleàl"unedesdroitesgénératrices

du cône; on a alors une courbe ouverte, laparabole. ˆSi nous inclinons encore plusP, le plan coupe le cône de part et d"autre de son sommet. On obtient une courbe ouverte constituée de deux branches, l"hyperbole. À la limite, si le plan passe parS, on obtient deux droites.

VII.d.2. Foyer, excentricité

On peut également définir les co-

niques de la manière suivante : considé- rons une droite(la "directrice»), un pointFet un nombree>0.

La conique defoyerFet

d"excentricitéeest l"ensemble des pointsMtels que k !FMkk !HMk=e; oùHest la projection orthogonale deM sur.

Sie<1, la conique est une ellipse

(en particulier un cercle sie=0); si e=1, c"est une parabole; sie>1, une

hyperbole.Si la conique est une ellipse ou une hyperbole, il existe un deuxième foyer,F0, et une deuxième

directrice,0, donnant la même courbe.

VII.d.3. Équation en coordonnées polaires

NotonsKla projection orthogonale deFsur,h=k!FKk,~ux=!FK=h(donck~uxk=1) et~uyun vecteur unitaire parallèle à.

Dans le repère orthonormé (F;~ux;~uy), l"équation en coordonnées polaires de la conique est

r=p1+ecos; oùrBk!FMk,B(~uxb;!FM) etpBe h.

Dans le cas de l"hyperbole, il s"agit de l"équation de la branche située en deçà de la directrice par

rapport àF. L"équation de la branche située au-delà est r=pecos1: 79

Michel FiocDynamique des systèmesDans un autre repère orthonormé (F;~ux0;~uy0), tourné de0par rapport à (F;~ux;~uy) (c.-à-d.(~ux0b;~ux)

=0), l"équation de la conique est r=p1+ecos(00);

où0B(~ux0b;!FM). De même, l"équation de la branche de l"hyperbole au-delà de la directrice est

r=pecos(00)1:

VII.d.4. Équation cartésienne

VII.d.4.a. Ellipse et hyperbole

Sie,1, la conique a un centre de symétrieOà mi-chemin des foyers. Posons a=pj1e2jetb=ppj1e2j:

VII.d.4.a.i. Ellipse

L"équation de l"ellipse dans le repère (O;~ux;~uy) (attention : l"origine n"est plusF) est x 2a 2+y2b 2=1; oùaest ledemi-grand axede l"ellipse etb(L"aire de l"ellipse vaut

A=a b:

VII.d.4.a.ii. Hyperbole

L"équation de l"hyperbole dans le repère (O;~ux;~uy) est x 2a 2y2b 2=1:

Pour tout pointMde l"hyperbole,

k!FMk k!F0Mk=2a: L"hyperbole a par ailleurs deux droites asymptotiques, d"équationsyasymp=(b=a)x. 80

Chapitre VII. Mouvements à force centrale

VII.d.4.b. Parabole

SoitSlesommetde la parabole, c.-à-d.le point de la parabole le plus proche de. Posons~uX=~uy et ~uY=~ux. L"équation de la parabole dans le repère (S;~uX;~uY) est

Y=X22p:

VII.e. Trajectoire

VII.e.1. Formules de Binet

Exprimonsv2en fonction deu=1=r. On a:=C=r2=C u2, donc v

2=:r2+r2:2=d[1=u]dt

2 +:2u 2= du=dtu 2 2 +:2u 2= du=du 2: 2 +:2u 2; d"où vquotesdbs_dbs6.pdfusesText_11

[PDF] 2eme loi de newton demonstration

[PDF] 2m maroc 1990

[PDF] 2m maroc programme

[PDF] 2m site

[PDF] 2nd year maths chapter 2 exercise 2.2

[PDF] 3 4 equivalent in cooking

[PDF] 3 as bac

[PDF] 3 commerce private colege in bbsr

[PDF] 3 commerce syllabus

[PDF] 3 ejemplos de indice

[PDF] 3 eme svt genetique

[PDF] 3 exemple qui illustre la puissance mondiale des etat unis

[PDF] 3 membranes de l'oeil

[PDF] 3*500 bac 2015

[PDF] 3*500 bac bareme 2017