FORMULAIRE d'INTÉGRATION Dans ce qui suit "c" est une
Dans ce qui suit "c" est une constante réelle. PRIMITIVES connues en terminale. ∫ a dx = ax + c. ∫ x dx = x2. 2. + c. ∫ xm dx =.
m
Second degré : Résumé de cours et méthodes 1 Définitions : 2
Racines : Une racine réelle dite "double" : x1 = − b. 2a . Factorisation : Pour tout x ax2 +bx+c = a(x−x1)2. Signe : ax2 +bx+
prem spe gen chap cours
MATRICES
Une matrice de taille 1 x m est appelée une matrice ligne. Exemple : Les coordonnées d'un vecteur du plan est une matrice colonne de dimension 2 x 1. a.
MatricesTESL
SECOND DEGRE (Partie 2)
Exemple : Le discriminant de l'équation 3x2 − 6x − 2 = 0 est : ∆ = (-6)2 – 4 x 3 x (-2) = 36 + 24 = 60. En effet a = 3
Secondegre ESL
ÉQUATIONS
x. EQUATION : c'est une opération « à trous » dont « les trous » sont remplacés par une 10 x 0625 - 2 = 2 x 0
Equations e
EQUATIONS INEQUATIONS
Le cas particulier de l'équation-produit (ax + b)(cx + d) = 0 équivaut à c) x2 − 9 x + 3. = 0 d) 1− x + 3 x − 3. = 2. 2 − x a) L'équation n'est pas ...
Equations Inequations
Considérons les matrices `a coefficients réels : A = - ( 2 1
AB est inversible d'inverse la matrice C. Montrer alors que B est inversible et préciser A-1. Exercice 13 – (extrait partiel novembre 2011). Soit X et Y
EC .
VECTEURS ET DROITES
2. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr Toute droite D admet une équation de la forme ax + by + c = 0 avec a ; b. ( )≠ 0;0.
VecteursDroites
Matrices
Calculer 3A+ 2C et 5B − 4D. Trouver α tel que A− αC soit la matrice nulle. 2. Montrer que si A+ B = A alors B est la matrice nulle
ch matrices
LES FONCTIONS DE REFERENCE
x. = − + est une fonction affine. La fonction g définie sur ℝ par. 2 p104 n°9 à 12 ... f x ax b. = + . Si. 0 a > alors f est croissante sur ℝ.
Fonctions reference
 Second degré : Résumé de cours et méthodes
Second degré : Résumé de cours et méthodes 1Définitions :
DÉFINITIONOn appelle trinôme du second degré toute fonctionfdéfinie surRparf(x) =ax2+bx+c(a,betcréels aveca6=0).Remarque :Par abus de langage, l"expressionax2+bx+cest aussi appelée trinôme du second degré.
DÉFINITIONOn appelle racine du trinômef, tout réel qui annulef.Exemple :1 est une racine du trinôme 2x2+3x5, car 2(1)2+3(1)5=0.
Remarque :Chercher les racines du trinômeax2+bx+c, revient à résoudre dansRl"équationax2+bx+c=0.
2Factorisation, racines et signe du trinôme :
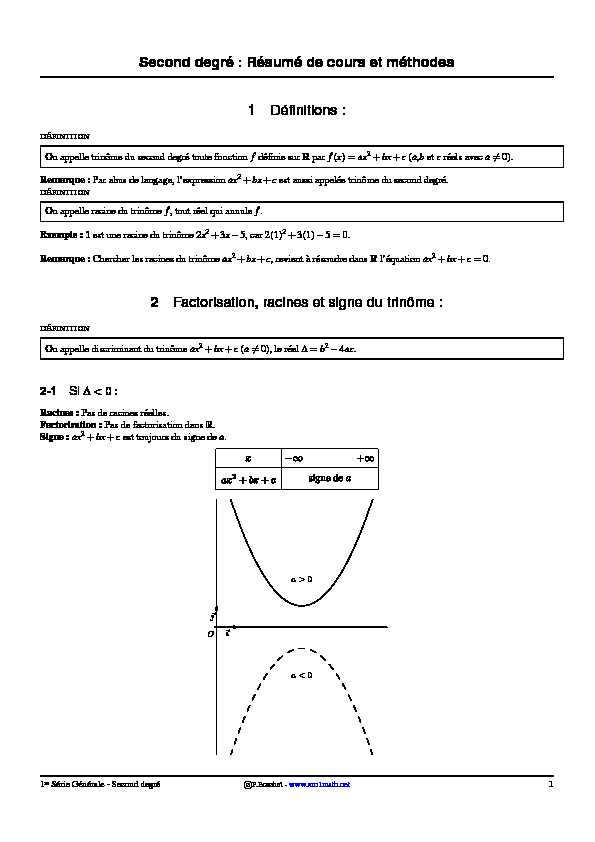
DÉFINITIONOn appelle discriminant du trinômeax2+bx+c(a6=0), le réelD=b24ac.2-1SiD<0:Racines :Pas de racines réelles.
Factorisation :Pas de factorisation dansR.
Signe :ax2+bx+cest toujours du signe dea.?
O?ı??a >0
a <01 reSérie Générale - Second degrécP.Brachet -www .xm1math.net1
2-2SiD=0:
Racines :Une racine réelle dite "double" :x1=b2a.Factorisation :Pour toutx,ax2+bx+c=a(xx1)2.
Signe :ax2+bx+cest toujours du signe deaet s"annule pourx=x1.?O?ı??a >0
a <0x12-3SiD>0:
Racines :Deux racines réelles :x1=bpD
2aetx2=b+pD
2aFactorisation :Pour toutx,ax2+bx+c=a(xx1)(xx2).
Signe :ax2+bx+cest du signe deaà l"extérieur des racines. (on suppose quex13Exemples de résolution d"équations et d"inéquations du second degré
3-1Equations du second degré
Résolution dansRde l"équationx2+2x3=0 :
(Par rapport aux formules, on a ici :a=1,b=2 etc=3 ).Calcul du discriminant :D=b24ac= (2)24(1)(3) =16.
Le discriminant est strictement positif, donc le trinôme admet deux racines réelles qui sont en fait les solutions de l"équa-
tion :Calcul des solutions :
x 1=bpD2a=2p16
21=242
=3x2=b+pD2a=2+p16
21=2+42
=1. L"ensemble solution est doncS=f3;1g.Résolution dansRde l"équation 2x22p2x+1=0 :
(Par rapport aux formules, on a ici :a=2,b=2p2 etc=1 ). Calcul du discriminant :D=b24ac= (2p2)24(2)(1) =428=0.Le discriminant est nul, donc le trinôme admet une seule racine réelle qui est en fait la solution de l"équation :
Calcul de la solution :
x1=b2a=(2p2)22=p2
2 . L"ensemble solution est doncS=( p2 2Résolution dansRde l"équation 3x2+4x+5=0 :
(Par rapport aux formules, on a ici :a=3,b=4 etc=5 ). Calcul du discriminant :D=b24ac=424(3)(5) =1660=44.Le discriminant est strictement négatif, donc le trinôme n"admet aucune racine réelle. L"ensemble solution est doncS=/0
Résolution dansRde l"équationx2+4x=0 :
(Par rapport aux formules, on a ici :a=1,b=4 etc=0 ).Comme à chaque fois queb=0 ouc=0, il est inutile d"utiliser le discriminant et les formules associées. Les méthodes
traditionnelles vues en Seconde sont plus simples et plus rapides. Ici, il suffit de factoriser parx:
x Second degré : Résumé de cours et méthodes1Définitions :
DÉFINITIONOn appelle trinôme du second degré toute fonctionfdéfinie surRparf(x) =ax2+bx+c(a,betcréels aveca6=0).Remarque :Par abus de langage, l"expressionax2+bx+cest aussi appelée trinôme du second degré.
DÉFINITIONOn appelle racine du trinômef, tout réel qui annulef.Exemple :1 est une racine du trinôme 2x2+3x5, car 2(1)2+3(1)5=0.
Remarque :Chercher les racines du trinômeax2+bx+c, revient à résoudre dansRl"équationax2+bx+c=0.
2Factorisation, racines et signe du trinôme :
DÉFINITIONOn appelle discriminant du trinômeax2+bx+c(a6=0), le réelD=b24ac.2-1SiD<0:Racines :Pas de racines réelles.
Factorisation :Pas de factorisation dansR.
Signe :ax2+bx+cest toujours du signe dea.?
O?ı??a >0
a <01 reSérie Générale - Second degrécP.Brachet -www .xm1math.net1
2-2SiD=0:
Racines :Une racine réelle dite "double" :x1=b2a.Factorisation :Pour toutx,ax2+bx+c=a(xx1)2.
Signe :ax2+bx+cest toujours du signe deaet s"annule pourx=x1.?O?ı??a >0
a <0x12-3SiD>0:
Racines :Deux racines réelles :x1=bpD
2aetx2=b+pD
2aFactorisation :Pour toutx,ax2+bx+c=a(xx1)(xx2).
Signe :ax2+bx+cest du signe deaà l"extérieur des racines. (on suppose quex13Exemples de résolution d"équations et d"inéquations du second degré
3-1Equations du second degré
Résolution dansRde l"équationx2+2x3=0 :
(Par rapport aux formules, on a ici :a=1,b=2 etc=3 ).Calcul du discriminant :D=b24ac= (2)24(1)(3) =16.
Le discriminant est strictement positif, donc le trinôme admet deux racines réelles qui sont en fait les solutions de l"équa-
tion :Calcul des solutions :
x 1=bpD2a=2p16
21=242
=3x2=b+pD2a=2+p16
21=2+42
=1. L"ensemble solution est doncS=f3;1g.Résolution dansRde l"équation 2x22p2x+1=0 :
(Par rapport aux formules, on a ici :a=2,b=2p2 etc=1 ). Calcul du discriminant :D=b24ac= (2p2)24(2)(1) =428=0.Le discriminant est nul, donc le trinôme admet une seule racine réelle qui est en fait la solution de l"équation :
Calcul de la solution :
x1=b2a=(2p2)22=p2
2 . L"ensemble solution est doncS=( p2 2Résolution dansRde l"équation 3x2+4x+5=0 :
(Par rapport aux formules, on a ici :a=3,b=4 etc=5 ). Calcul du discriminant :D=b24ac=424(3)(5) =1660=44.Le discriminant est strictement négatif, donc le trinôme n"admet aucune racine réelle. L"ensemble solution est doncS=/0
Résolution dansRde l"équationx2+4x=0 :
(Par rapport aux formules, on a ici :a=1,b=4 etc=0 ).Comme à chaque fois queb=0 ouc=0, il est inutile d"utiliser le discriminant et les formules associées. Les méthodes
traditionnelles vues en Seconde sont plus simples et plus rapides. Ici, il suffit de factoriser parx:
x