Fonctions logarithmes népérien et décimal
La fonction logarithme népérien notée ln
TS courslogarithme
La fonction logarithme décimal
La fonction logarithme décimal. Propriétés analytiques. Pour x strictement positif log(x) = ln(x) ln(10). (avec ln(10) = 2
LogarithmeDecimal
CHAPITRE 11 : FONCTION NEPERIEN. FONCTION LOGARITHME
FONCTION. LOGARITHME DECIMAL. 1. Fonction népérien (logarithme d'une fonction composée). Théorème. Si u
cours chap
FONCTION LOGARITHME NEPERIEN
fonction logarithme décimale notée log est définie par : log(x) = lnx ln10. Conséquences : a) y = lnx avec x > 0 ⇔ x = ey b) ln1= 0 ; lne = 1 ; ln.
LogTS
FONCTION LOGARITHME DÉCIMAL
Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. FONCTION LOGARITHME DÉCIMAL. En 1614 un mathématicien écossais
LogTT
FONCTION LOGARITHME NÉPÉRIEN (Partie 1)
Ceci peut paraître dérisoire aujourd'hui mais il faut comprendre qu'à cette époque
LogT
LOGARITHME NEPERIEN
On note a = ln b ce qui se lit logarithme népérien de b . On appelle fonction logarithme décimal et on note log la fonction définie sur ] 0 ...
ln
Logarithme décimal et acoustique (calculatrice algorithme)
Votre voisin François chanteur amateur
logaritme decimal et acoustique
Etude des besoins mathématiques en physique et en chimie
https://pedagogie.ac-orleans-tours.fr/fileadmin/user_upload/maths/Dossiers_acad%C3%A9miques/Progressions/TermS/2-Lien_2_Logarithmes_pour_le_physicien.pdf
Formulaire : La fonction logarithme népérien
Formulaire : La fonction logarithme népérien. • Fonction continue et dérivable sur ]0;+∞[ Propriétés de la fonction logarithme décimal. • log(10) = 1.
Formulaire logarithme
1 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr FONCTION LOGARITHME NÉPÉRIEN
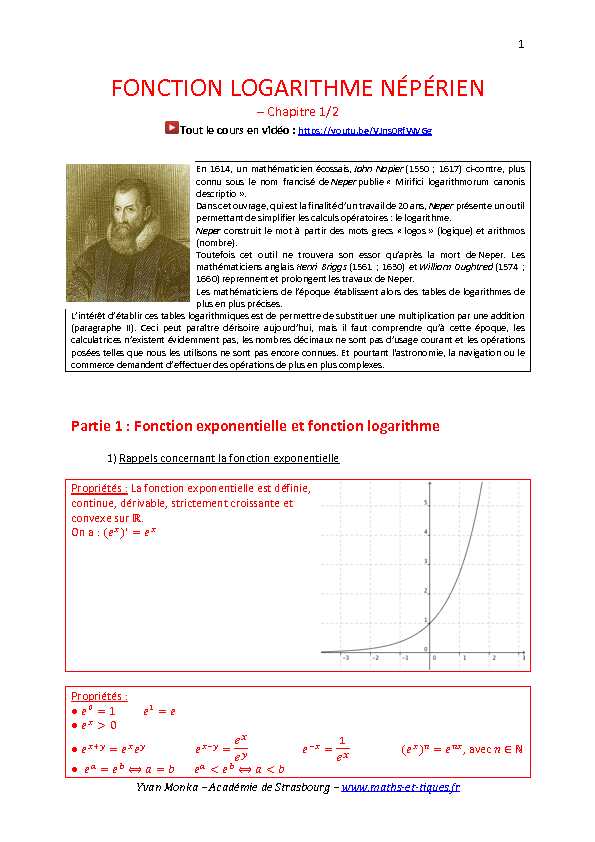
- Chapitre 1/2 Tout le cours en vidéo : https://youtu.be/VJns0RfVWGg En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie " Mirifici logarithmorum canonis descriptio ». Dans cet ouvrage, qui est la finalité d'un travail de 20 ans, Neper présente un outil permettant de simplifier les calculs opératoires : le logarithme. Neper construit le mot à partir des mots grecs " logos » (logique) et arithmos (nombre). Toutefois cet outil ne trouve ra son essor qu'après la mort de Neper. Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ;1660) reprennent et prolongent les travaux de Neper.
Les mathématiciens de l'époque établissent alors des tables de logarithmes de plus en plus précises.L'intérêt d'établir ces tables logarithmiques est de permettre de substituer une multiplication par une addition
(paragraphe II). Ceci peut paraître dériso ire aujourd'hui , mais il faut co mprendre qu'à cette époque, les
calculatrices n'existent évidemment pas, les nombres décimaux ne sont pas d'usage courant et les opérations
posées telles que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le
commerce demandent d'effectuer des opérations de plus en plus complexes. Partie 1 : Fonction exponentielle et fonction logarithme1) Rappels concernant la fonction exponentielle
Propriétés : La fonction exponentielle est définie, continue, dérivable, strictement croissante et convexe sur ℝ.On a :
Propriétés :
=1 >0 , avec ∈ℕ 2 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr2) Définition de la fonction logarithme népérien
La fonction exponentielle est continue et strictement croissante sur ℝ, à valeurs dans0;+∞
D'après le théorème des valeurs intermédiaires, pour tout réel de0;+∞
l'équation = admet une unique solution dans ℝ.Définitions : On appelle logarithme népérien d'un réel strictement positif , l'unique
solution de l'équation =. On la note ln. La fonction logarithme népérien, notée , est la fonction définie sur0;+∞
, par ⟼ln()Remarques :
- Les fonctions et sont réciproques l'une de l'autre. - Les courbes représentatives des fonctions et sont symétriques par rapport à la droite d'équation =. 1 2 0 (2) 1 2 expln 3 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr - Dans le domaine scientifique, on utilise la fonction logarithme décimale, notée log, et définie par : log()= Propriétés de ln liées à la fontion exp : a) Pour >0 : = ⇔=ln() b) ln(1)=0 ; ln()=1 ; lnD 1 E=-1 c) ln( d) Pour >0 :Démonstrations :
a) Par définition b) - =1 donc d'après a, on a : ln(1)=0 = donc d'après a, on a : ln()=1 1 donc d'après a, on a : lnD 1 E=-1 c) Si on pose = , d'après a, on a : =ln()=ln( d) Si on pose =ln(), d'après a, on a : = Partie 2 : Propriétés de la fonction logarithme népérien1) Relation fonctionnelle
Théorème : Pour tous réels et strictement positifs, on a : ln =ln()+ln()Démonstration :
Donc : ln
1 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.frFONCTION LOGARITHME NÉPÉRIEN
- Chapitre 1/2 Tout le cours en vidéo : https://youtu.be/VJns0RfVWGg En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie " Mirifici logarithmorum canonis descriptio ». Dans cet ouvrage, qui est la finalité d'un travail de 20 ans, Neper présente un outil permettant de simplifier les calculs opératoires : le logarithme. Neper construit le mot à partir des mots grecs " logos » (logique) et arithmos (nombre). Toutefois cet outil ne trouve ra son essor qu'après la mort de Neper. Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ;1660) reprennent et prolongent les travaux de Neper.
Les mathématiciens de l'époque établissent alors des tables de logarithmes de plus en plus précises.L'intérêt d'établir ces tables logarithmiques est de permettre de substituer une multiplication par une addition
(paragraphe II). Ceci peut paraître dériso ire aujourd'hui , mais il faut co mprendre qu'à cette époque, les
calculatrices n'existent évidemment pas, les nombres décimaux ne sont pas d'usage courant et les opérations
posées telles que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le
commerce demandent d'effectuer des opérations de plus en plus complexes. Partie 1 : Fonction exponentielle et fonction logarithme1) Rappels concernant la fonction exponentielle
Propriétés : La fonction exponentielle est définie, continue, dérivable, strictement croissante et convexe sur ℝ.On a :
Propriétés :
=1 >0 , avec ∈ℕ 2 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr2) Définition de la fonction logarithme népérien
La fonction exponentielle est continue et strictement croissante sur ℝ, à valeurs dans0;+∞
D'après le théorème des valeurs intermédiaires, pour tout réel de0;+∞
l'équation = admet une unique solution dans ℝ.Définitions : On appelle logarithme népérien d'un réel strictement positif , l'unique
solution de l'équation =. On la note ln. La fonction logarithme népérien, notée , est la fonction définie sur0;+∞
, par ⟼ln()Remarques :
- Les fonctions et sont réciproques l'une de l'autre. - Les courbes représentatives des fonctions et sont symétriques par rapport à la droite d'équation =. 1 2 0 (2) 1 2 expln 3 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr - Dans le domaine scientifique, on utilise la fonction logarithme décimale, notée log, et définie par : log()= Propriétés de ln liées à la fontion exp : a) Pour >0 : = ⇔=ln() b) ln(1)=0 ; ln()=1 ; lnD 1 E=-1 c) ln( d) Pour >0 :Démonstrations :
a) Par définition b) - =1 donc d'après a, on a : ln(1)=0 = donc d'après a, on a : ln()=1 1 donc d'après a, on a : lnD 1 E=-1 c) Si on pose = , d'après a, on a : =ln()=ln( d) Si on pose =ln(), d'après a, on a : = Partie 2 : Propriétés de la fonction logarithme népérien1) Relation fonctionnelle
Théorème : Pour tous réels et strictement positifs, on a : ln =ln()+ln()Démonstration :
Donc : ln
- relation logarithme décimal et népérien