[PDF] Analyse Numérique : SMA-SMI S4 Cours exercices et examens

View - Download Analyse Numérique : SMA-SMI S4 Cours exercices et examens

Previous PDF

Next PDF

Analyse Numérique: SMA-SMI S4Cours, exercices et examens

Boutayeb A, Derouich M, Lamlili M et Boutayeb W.

Table des matières1 Résolution numérique de systèmes linéairesAX=B5

1.1 Méthodes directes de résolution de AX=B . . . . . . . . . . . . . . .. 5

1.1.1 Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.1.2 Méthode de Gauss(avec et sans pivot) . . . . . . . . . . . . . . 7

1.1.3 Factorisation LU . . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.1.4 Factorisation de Choleski (matrice symétrique) . . . .. . . . . 13

1.1.5 Factorisation de Householder (matrice unitaire ) . . .. . . . . 14

1.2 Méthodes indirectes de résolution de AX=B . . . . . . . . . . . . .. . 15

1.2.1 Quelques rappels sur les matrices . . . . . . . . . . . . . . . . 15

1.2.2 Méthodes classiques(Jacobi, Gauss Seidel, Relaxation) . . . . 15

1.3 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

2 Approximations des solutions de l"équationf(x) =022

2.1 Rappels et notations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

2.2 Méthode de Newton : . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

2.3 Méthode de Newton modifiée : . . . . . . . . . . . . . . . . . . . . . . 29

2.4 Méthode de dichotomie : . . . . . . . . . . . . . . . . . . . . . . . . . 29

2.5 Méthode de fausse position ( Regula Falsi) : . . . . . . . . . . . .. . 31

2.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

3 Inroduction à l"interpolation36

3.1 Rappel et définitions . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

3.2 Interpolant de Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . 36

3.3 Interpolant de Newton . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

3.4 Existence et Unicité de l"interpolant . . . . . . . . . . . . . . .. . . . 41

3.4.1 Interpolation linéaire . . . . . . . . . . . . . . . . . . . . . . . . 42

3.5 Erreur d"interpolation . . . . . . . . . . . . . . . . . . . . . . . . . . .43

3.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

1

4 Intégration numérique46

4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

4.2 Approximation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

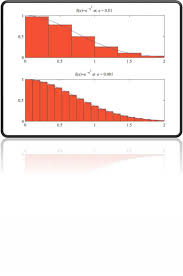
4.2.1 Approximation par des rectangles à gauche . . . . . . . . . .. 48

4.2.2 Approximation par des rectangles à droite . . . . . . . . . .. 49

4.2.3 Approximation par des rectangles médians . . . . . . . . . .. 50

4.2.4 Approximations par des trapèzes . . . . . . . . . . . . . . . . . 51

4.2.5 Formule de Simpson . . . . . . . . . . . . . . . . . . . . . . . . 52

4.3 Interpolation et Erreur d"intégration numérique . . . . .. . . . . . . 53

4.3.1 Interpolation linèaire et la formule du trapèze : . . . .. . . . . 53

4.3.2 Formule du trapèze composée . . . . . . . . . . . . . . . . . . 53

4.3.3 Erreur de la formule de Simpson . . . . . . . . . . . . . . . . . 54

4.4 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

5 Analyse numérique des équations differentielles ordinaires (e.d.o) 56

5.1 Rappels sur les équations differentielles ordinaires (e.d.o) . . . . . . 56

5.2 Systèmes linéaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

5.3 Notions de stabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58

5.4 Systèmed"équationsauxdifferenceslinéaires aveccoéfficientsconstants 60

5.5 Méthodes numériques pour les problèmes de condition initiale . . . 61

5.5.1 Convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

5.5.2 Consistance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

5.5.3 Stabilité . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

5.5.4 Méthode d"Euler . . . . . . . . . . . . . . . . . . . . . . . . . . 64

5.5.5 Méthodes de Taylor dans le cas scalaire . . . . . . . . . . . . . 66

5.5.6 Méthodes de Runge-Kutta (R.K) dans le cas scalaire . . . . . .67

5.5.7 Méthodes de Runge-Kutta explicites . . . . . . . . . . . . . . . 67

5.6 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

6 Examens77

6.1 F.S.O Session ordinaire 2012-2013 (Durée : 1h30) . . . . . .. . . . . . 77

6.2 F.S.O Session Rattrapage 2012-2013 (Durée : 1h30) . . . . .. . . . . . 79

6.3 F.S.O Session ordinaire 2011-2012 (Durée : 1h30) . . . . . .. . . . . . 81

6.4 F.S.O Session de rattrapage 2011-2012 (Durée : 1h30) . . .. . . . . . . 83

6.5 F.S.O Session ordinaire 2010-2011 (Durée :1h30) . . . . . .. . . . . . . 85

6.6 F.S.O Session Rattrapage 2010-2011 (Durée : 1h30) . . . . .. . . . . . 87

6.7 F.S.O Examen 2009-2010 . . . . . . . . . . . . . . . . . . . . . . . . . . 89

6.8 F.S.O Session ordinaire 2008/2009 . . . . . . . . . . . . . . . . . .. . 91

2

6.9 F.S.O Session rattrapage 2008-2009 . . . . . . . . . . . . . . . . .. . . 93

6.10 F.S.O Session ordinaire 2007-2008(Durée : 1h30) . . . . .. . . . . . . . 94

6.11 F.S.O Examen blanc 2007-2008 . . . . . . . . . . . . . . . . . . . . . .. 96

6.12 F.S.O Devoir à faire chez soi 2007-2008 . . . . . . . . . . . . . .. . . . 98

6.13 F.S.O Session ordinaire Janvier 2003 . . . . . . . . . . . . . . .. . . . 99

3

Table des figures

2.1la solution estx=1.3652 . . . . . . . . . . . . . . . . . . . . . . . . . 29

2.2f(1).f(2)<0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

2.3x=2.7133 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

3.1Interpolation de Newton. . . . . . . . . . . . . . . . . . . . . . . . . 41

3.2Interpolation de Lagrange. . . . . . . . . . . . . . . . . . . . . . . . 44

4.1 Approximation par des rectangles à gauche . . . . . . . . . . . .. . . 49

4.2 Approximation par des rectangles à droite . . . . . . . . . . . .. . . . 50

4.3 Approximation par des rectangles médians . . . . . . . . . . . .. . . 51

4 Chapitre 1Résolution numérique de systèmeslinéairesAX=B

1.1 Méthodes directes de résolution de AX=B

1.1.1 Exemples

1. Résoudre(S):?

x

1-x2=0L1

x

1+x2=2L2

Par substitution

L

1→x1=x2

L

2→2x1=2→x1=1→x2=x1=1

Par combinaison de lignes

L

1→x1-x2=0

L

Par Inversion de la matrice

(S)? 1-1

1 1? ?

x 1 x 2? 0 2? AX=B detA=2;A-1=1 detAt comA=12? 1 1 -1 1?

SiA-1existe alorsX=A-1B

x 1 x 2? =(((1 212
-1

212)))

0 2? 1 1? par méthode de Cramer 5 +13x2+5x3+4x4=0L2 -2x3+5x4=8L3

7x4=14L4

(S)((((((4 15 3-17

0 13 5 4

0 0-2 5

0 0 0 7))))))

x 1 x 2 x3 x4)))))) =((((((-18 0 8

14))))))

Résolution par remontée ( en commençant parx4) L

4→x4=14

7=2 L

3→x3=(8-5×2)

-2=1 L

2→x2=(0-4×2-5×1)

13=-1 L

1→x1=(-18+17×2-3×1+15×1)

4=7

3. Système triangulaire : cas général

ST

11x1+u12x2+···+u1nxn=b1L1

u

22x2+···+u2nxn=b2L2...

u x 1 x 2 x n)))))) =((((((b 1 b 2 b n))))))

On suppose queukk?=0k=1,···,n

x n=bn unn x n-1= (bn-1-unnbn)/un-1n-1 x i= (bi-∑j=n j=i+1uijbj)/uiii=n-1,....1

Algorithme de résolution pourUX=B

x n=bn unnPouri=n-1 à 1 x i=bi

Pourj=i+1 àn

x i=xi-uijxj Fin j Fin i

Remarques 1.1.1.Remarques :

1. La matrice U est dite triangulaire supérieure. Elle est inversible si tous les

termes diagonaux sont non nuls et detU=u11?u22? ··· ?unn 6

2. La matrice triangulaire inférieure se traite de façon similaire

3. le nombre d"opérations nécéssaires est :

n(n-1)

1.1.2 Méthode de Gauss(avec et sans pivot)

Elle consisteàramenerunsystèmelinéaire dela formeAX=B(Aavec matrice pleine) à un système de la formeUX=Dpuis à résoudre ce dernier.

Exemple 1.1.1.Résoudre

(S?):?????3x1+5x2+2x3=8L1

0x1+8x2+2x3=-7L2

6x1+2x2+8x3=26L3

Etape1:

?3x1+5x2+2x3=8L(1) 1=L1

0+8x2+2x3=-7L(1)

2=L2

0-8x2+4x3=10L(1)

3=L3-2L1?????

Etape2:

?3x1+5x2+2x3=8L(1) 1=L1quotesdbs_dbs13.pdfusesText_19

[PDF] analyse numérique exercices corrigés méthode de newton pdf

[PDF] analyse numérique exercices et problèmes corrigés

[PDF] analyse numérique interpolation polynomiale exercices corrigés

[PDF] analyse numérique matricielle exercices corrigés pdf

[PDF] analyse numérique matricielle pdf

[PDF] analyse numérique pour ingénieurs

[PDF] analyse physico chimique du lait cru pdf

[PDF] analyse physico chimique du lait de vache pdf

[PDF] analyse physico chimique du lait en poudre

[PDF] analyse physico chimique du lait ppt

[PDF] analyse physico chimique du miel

[PDF] analyse physico-chimique des dattes

[PDF] analyse psychologique gratuite

[PDF] analyse séquentielle des politiques publiques

[PDF] analyse sociologique film ressources humaines