[PDF] Introduction au principe variationnel et `a la mécanique analytique

View - Download Introduction au principe variationnel et `a la mécanique analytique

Previous PDF

Next PDF

Introduction au principe variationnel et a la

mecanique analytiqueNotes de Cours de LicenceL3-Phytem

Nicolas Sator

Laboratoire de Physique Theorique de la Matiere Condensee

Universite Pierre et Marie Curie Paris 6

LPTMC - Octobre 2017

Depuis le XVII eme siecle, l'approche variationnelle permet de decrire des phenomenes physiques a l'aide d'un principe d'economie, appele en optiqueprincipe de Fermatet en mecaniqueprincipe de moindre action: le comportement observe d'un systeme correspond a la minimisation (ou a la maximisation) d'une certaine grandeur. Ce cadre abstrait et general permet une reformulation simple et elegante de nombreux problemes en physique (optique geometrique, mecanique classique, mecanique quantique, relativite, electromagnetisme). Mais au-dela de considerations esthetiques ou techniques, l'approche variationnelle forme la pierre angulaire de la physique statistique, de la theorie du chaos et de la theorie des champs. Dans ces notes de cours, nous aborderons quelques notions de calcul variationnel (et en particulier les equations d'Euler-Lagrange) que nous appliquerons par la suite dans le cadre de la mecanique analytique.

Bibliographie

|Le principe de moindre action et les principes variationnels en physique, J.-L. Bas- devant (Vuibert, 2010) |Mecanique quantique, 1. Fondements et premieres applications, C. Aslangul (de

Boeck, 2007), chapitre 7

|Le cours de physique de Feynman, tome 1 :Electromagnetisme, R. Feynman (Dunod,

1999), chapitre 19

|Mecanique, L. Landau et E. Lifchitz (Mir, Moscou, 1982) |Mecanique, De la formulation Lagrangienne au chaos Hamiltonien, C. Gignoux et

B. Silvestre-Brac (EDP Sciences, 2002)

|Mecanique analytique, R. Dandolo (Publibook, 2005)

Table des matieres

I Introduction : le principe de Fermat 4

II Approche variationnelle 5

1 L'equation d'Euler-Lagrange . . . . . . . . . . . . . . . . . . . . . . . . . . 6

a Notion de fonctionnelle . . . . . . . . . . . . . . . . . . . . . . . . . 6 b Demonstration de l'equation d'Euler-Lagrange . . . . . . . . . . . . 6 c Formule de Beltrami . . . . . . . . . . . . . . . . . . . . . . . . . . 7 d Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2 L'Approche variationnelle avec des contraintes . . . . . . . . . . . . . . . . 9

a Methode des multiplicateurs de Lagrange . . . . . . . . . . . . . . . 10 b Contraintes de type holonome . . . . . . . . . . . . . . . . . . . . . 13 c Contraintes de forme integrale . . . . . . . . . . . . . . . . . . . . . 14 2

IIIRudiments de mecanique analytique 17

1 De Newton a Lagrange : une reformulation de la mecanique . . . . . . . . 17

2 Le formalisme Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

a Le principe de moindre action . . . . . . . . . . . . . . . . . . . . . 17 b Le Lagrangien . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

3 Le formalisme hamiltonien . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

a Les equations de Hamilton . . . . . . . . . . . . . . . . . . . . . . . 21 b L'espace des phases . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 c Les crochets de Poisson . . . . . . . . . . . . . . . . . . . . . . . . 24

4 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

5 Exercices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

a L'oscillateur harmonique . . . . . . . . . . . . . . . . . . . . . . . . 27 b La bille et le cerceau . . . . . . . . . . . . . . . . . . . . . . . . . . 28 c L'atome hydrogenode . . . . . . . . . . . . . . . . . . . . . . . . . 30 d La particule chargee dans un champ electromagnetique . . . . . . . 32 e Le theoreme du viriel . . . . . . . . . . . . . . . . . . . . . . . . . . 34 3

I Introduction : le principe de Fermat

Les lois de l'optique geometrique { propagation rectiligne de la lumiere dans un milieu homogene, principe de retour inverse de la lumiere et lois de la re exion et de la refraction de Snell (1621), Descartes (1637) et Ibn Sahl

1(984){ ont une origine phenomenologique.

En 1661, Pierre de Fermat (1601-1665) propose une autre approche, plus abstraite, basee sur l'idee que \La nature agit toujours par les voies les plus courtes et les plus simples"2. Le principe de Fermat s'enonce comme un principe de moindre temps3, ou \d'economie naturelle" : La lumiere se propage d'un point a un autre sur des trajectoires telles que la duree du parcours est stationnaire. Il s'agit bien d'un principe variationnel car la duree du parcours doit ^etre extremale, en generale minimale, par rapport a une petite variation du trajet. A l'aide de ce principe, on demontre immediatement la loi de propagation rectiligne de la lumiere dans un milieu homogene. Les lois de l'optique geometrique se reformulent a la Feynman par une analogie cinematique.

Le probleme du ma^tre nageur

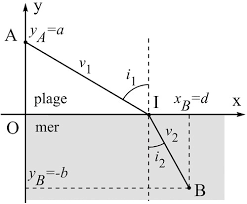
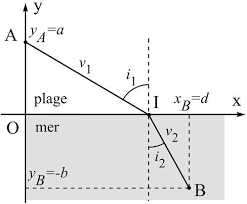
Telle la lumiere qui se propage moins vite dans l'eau que dans l'air, un ma^tre nageur court plus vite qu'il ne nage. Il se trouve au pointAlorsqu'il apercoit une jolie lle qui se noie enB. Comment arriver enBle plus vite possible? Sachant que le ma^tre nageur court en ligne droite a la vitessev1et nage a la vitessev2< v1, quel est le pointIou il doit plonger? Il faut trouver un compromis entre la ligne droite entreAetBet le parcours qui rend minimale la distance parcourue dans l'eau. Figure1 {Le probleme du ma^tre nageur enAet de la lle qui se noie enB. Comme on le voit sur la gure 1, la trajectoire du ma^tre nageur est constituee de deux

droites AI et IB, ouI(x;0) est le point ou le ma^tre nageur plonge. A priori la distance1. En eet, le mathematicien persan Ibn Sahl a decouvert la loi de la refraction des 984.

2. Plus exactement son principe de moindre temps s'enonce : \Il n'y a rien de si probable ni de si apparent que cette

supposition, que la nature agit toujours par les moyens les plus aises, c'est-a-dire ou par les lignes les plus courtes,

lorsqu'elles n'emportent pas plus de temps, ou en tout cas par le temps le plus court, an d'accourcir son travail et de venir

plus t^ot a bout de son operation\. La reaction du cartesien de Clerselier (dans une lettre a Fermat en 1662) est egalement

instructive : \Le principe que vous prenez pour fondement de votre demonstration, a savoir que la nature agit toujours par

les voies les plus courtes et les plus simples, n'est qu'un principe moral et non point physique, qui n'est point et qui ne peut

^etre la cause d'aucun eet de la nature".

3. Une formulation plus moderne repose sur la notion de chemin optique (L=R

Cndl, oun=c=vest l'indice de refraction

etcla vitesse de la lumiere dans le vide) : Le trajet suivi par la lumiere entre deux pointsAetBest celui qui correspond

a une valeur stationnaire du chemin optique. 4 AI sera plus grande que la distance IB car il court plus vite qu'il ne nage. Le tempsT(x) mis par le ma^tre nageur pour aller deAenBest : T=AIv 1+IBv 2 soit,

T(x) =px

2+a2v

1+p(dx)2+b2v

2: Le temps est minimal (il ne peut pas s'agir d'un maximum!) quand dTdx =1v 1xpx

2+a21v

2dxp(dx)2+b2= 0;

soit 1v

1sin(i1) =1v

2sin(i2):

La vitesse de la lumiere dans un milieu d'indice de refractionnetantv=c=n, oucest la vitesse dans le vide, on retrouve la loi de la refraction de Ibn Sahl-Snell-Descartes-Fermat (Fermat a utilise lui une demonstration geometrique). On montrerait de m^eme la loi de la re exion.

II Approche variationnelle

Dans le cas de la loi de la refraction, la trajectoire du rayon lumineux etait determinee par la valeur dexqui minimiseT(x). En general, c'est toute une fonction (par exemple une trajectoire) que l'on recherche. Par exemple, quel est le plus court chemin entre deux pointsAetBd'un plan?BA xy dy dxdsFigure2 {Le chemin le plus court entre deux pointsAetB. En notantsl'abscisse curviligne le long d'un chemin, on a ds=pdx

2+dy2=p1 +y02dx;

5 ouy0(x) =dydx . La longueurldu chemin est donnee par l[y] =Z B A ds=Z xB x

Ap1 +y02dx:

On cherche donc la fonctiony(x) qui rend l'integralel[y] minimale telle quey(xA) = y(xB) =cte. La reponse est bien s^ury(x) =cte, mais comment le demontrer?

1 L'equation d'Euler-Lagrange

a Notion de fonctionnelle La fonctionnelle est une generalisation de la fonction. Plut^ot que de dependre d'une (ou plusieurs) variable, une fonctionnelle depend d'une (ou plusieurs) fonction, elle m^eme dependant d'une (ou plusieurs) variable. C'est donc une \fonction de fonction". Considerons une fonctiony(x) dependant d'une variablexet une fonctionfa trois va- riables non independantesfy(x);y0(x);x, ouy0(x) =dydx . La fonctiony(x) etant connue, la fonctionfprend donc une valeur determinee pour une valeur dexdonnee. Nous verrons que la dependance en la deriveey0(x) intervient frequemment, en particulier en mecanique. Remarquons que la fonctionfdepend dexexplicitement, mais aussi implicitement a tra- versy(x) ety0(x). La derivee totale defpar rapport axest donc : dfdx =@f@x +@f@y dydx +@f@y 0dy 0dx =@f@x +@f@y y0+@f@y 0y00:

Denissons la fonctionnelleS[y] par l'integrale :

S[y]Z x2 x

1fy(x);y0(x);xdx:

La fonctionnelleS[y] est donc un nombre qui depend de la fonctiony(x). L'approche varia- tionnelle va nous permettre de determiner la fonctiony(x) telle queS[y] soit stationnaire (extremale), sachant quey(x1) ety(x2) sont donnes. Nous allons montrer que la fonctiony(x) qui remplit cette condition verie l'equation d'Euler-Lagrange 4:@f @y ddx @f@y

0= 0:b Demonstration de l'equation d'Euler-Lagrange

Supposons que l'on connaisse la fonctiony0(x) qui rendeSextremale et considerons une petite variation de chemin y(x) =y0(x) + (x); ou(x) est une fonction telle que(x1) =(x2) = 0 et1. Alors la fonctionnelle associee au cheminy(x) parametre pars'ecrit

S() =Z

x2 x 1f y

0(x) + (x);y00(x) + 0(x);x

dx:4. Leonhard Euler (1707-1783) mathematicien et physicien suisse. 6

Derivons par rapport a

dSd () =Z x2 x 1dd f y

0(x) + (x);y00(x) + 0(x);x

dx Z x2 x 1 @f@y @y@ +@f@y 0@y 0@ dx Z x2 x 1 @f@y (x) +@f@y 00(x) dx: En integrant par parties la seconde integrale, on obtient : dSd () =Z x2 x 1 (x)@f@y (x)ddx @f@y 0 dx+(x)@f@y 0 x2 x 1: Puisque(x1) =(x2) = 0, le dernier terme de l'equation s'annule. Et comme la fonc- tionnelleS() est extremale pour la fonctiony0, sa derivee doit s'annuler en= 0 donc dSd (0) =Z x2 x

1(x)@f@y

ddx @f@y 0 dx= 0 et ce, quelle que soit la fonction(x). On en deduit l'equation d'Euler-Lagrange : @f@y ddx @f@y 0= 0: c Formule de Beltrami Si la fonctionfne depend pas explicitement de la variablex, (@f@x = 0), on obtient la formule de Beltrami : fy0@f@y

0=C;(1)

ouCest une constante. Pour demontrer cette formule, calculons ddx fy0@f@y

0=@f@y

y0+@f@y

0y00y00@f@y

0y0ddx

@f@y 0 |{z} @f@y = 0; en utilisant l'equation d'Euler-Lagrange. d Exemples

Le chemin le plus court

On cherche le cheminy(x) qui minimise la longueur

l[y] =Z xB x

Af(y0)dx;

ouf(y0) =p1 +y02avecy(xA) =y(xB) =cte. Puisquefne depend pas dey, on a d'apres l'equation d'Euler-Lagrange : @f@y

0=y0p1 +y02=C;

7 ouCest une constante. On trouve doncy0=cte, autrement dit, l'equation d'une droite qui passe par les pointsAetB. Dans cet exemple la reponse etait evidente, mais l'approche variationnelle est tres utile lorsque l'espace-temps est dote d'une metrique plus complexe dans le cadre de la theorie de la relativite.

La courbe brachistochrone

La courbe brachistochrone

5a ete etudiee par Leibniz, Newton, Jacques et Jean Ber-

noulli et Euler : En partant d'une position donnee sans vitesse initiale, quelle est la trajectoire qui permet d'atteindre le plus rapidement possible une position nale dans le champ de pesanteur? Pour preciser les notations, supposons que l'objet parte du pointAde coordonnees x A= 0 etyA=h >0, sans vitesse initiale et glisse le long d'un toboggan jusqu'au point Bde coordonneesxB=d >0 etyB= 0 (voir la gure 3). On doit donc exprimer la duree du parcours entreAetB, puis chercher la courbe (la forme du toboggan) qui minimise cette duree.xy A Bh

dFigure3 {Un objet part du pointAsans vitesse initiale et glisse le long de la courbe jusqu'au pointB.

Soitsl'abscisse curviligne, unelement de courbedss'exprime en coordonnees cartesiennes ds=pdx

2+dy2=p1 +y02dx;

ouy0=dydx . La vitesse de l'objet est donnee parv=dsdt . La conservation de l'energie mecanique implique12 mv2+mgy=mgh: Exprimons le temps de parcoursT[y]. C'est une fonctionnelle qui depend de la formey(x) du toboggan. On a dt=dsv =p1 +y02dxv =p1 +y02p2g(hy)dx:

Le temps de parcours s'ecrit donc :

T[y] =Z

d 0 f(y;y0)dx;5. En grec, \Brakhisto" signie "le plus court" et \chronos", le temps. 8 ouf(y;y0) =s1 +y022g(hy)ne depend pas dex. On cherche donc la formey(x) qui minimise la fonctionnelleT[y]. Puisquefest independante dex, on peut utiliser la formule de

Beltrami

fy0@f@y 0=C; ouCest une constante. Donc

1p1 +y02=Cp2g(hy):

En elevant au carre on a donc :

1 +y02=Rhy;

ouR= 1=2gC2. Posonsy0= tan(=2) :

1 +y02= 1 + tan22

=1cos 22
=Rhy; soit y=hRcos22 =hR2 (1 + cos):

Par ailleurs,

y

0= tan(=2) =dydx

=dyd ddx =R2 sinddx =Rsin2 cos2 ddx donc dx=Rcos22 d; soit en integrant x=R2 (+ sin) +cteety=hR2 (1 + cos); que l'on peut ecrire avec le changement de variable!et en imposantx(0) = 0 : x=R2 (sin) ety=hR2 (1cos): C'est l'equation d'une cyclode. Reste a determinerRpour que la trajectoire passe par le pointB. Sur la gure 4, on remarque que la pente a l'origine est innie pour obtenir une acceleration initiale maximale

2 L'Approche variationnelle avec des contraintes

Dans un probleme aux variations, il peut exister une (ou plusieurs) contrainte sur la fonctiony(x). Le probleme isoperimetrique en est une belle illustration : Dans le plan, quelle est la courbe fermee qui a la plus grande aire pour un perimetre donne? Dans le plan muni d'un repere cartesien, on cherche l'equationy(x) de cette courbe telle que l'aire

A[x;y] =I

ydx(2) 9 -0.2 0 0.2 0.4 0.6 0.8 1 0 0.5 1 1.5 2 y xFigure4 {La courbe brachistochrone entre le pointA(0;1)et le pointB(2;0)pourR'1:035. soit maximale avec la contrainte suivante : le perimetre l[x;y] =Ip1 +y02dx(3) est xe. a Methode des multiplicateurs de Lagrange Pour simplier, nous raisonnerons dans un premier temps a l'aide d'unefonctionde plusieurs variables. La generalisation a la fonctionelle ne posant pas de probleme. Par exemple, un fabriquant souhaite produire un recipient cylindrique de volume xe V

0dont la surfaceSsoit la plus faible possible (pour minimiser la quantite de materiaux).

Comment choisir la hauteurLet le rayonRdu cylindre? La surface est une fonction deLetR:S(L;R) = 2R2+2RL. On cherche le minimum deSavec la contrainteV(L;R) =R2L=V0. En remplacantL=V0=R2dansS(L;R) on se ramene facilement a une fonction a une variable dont il est facile de trouver le minimum obtenu pourR= (V0=2)1=3, soit un rapportL= 2R(qui se rapproche le plus d'une sphere). Generalisons, soitf(x1;x2;;xn) une fonction denvariables. Pour quefsoit extremale en un certain pointx01;x02;:::;x0n, il faut que df=X i@f@x idx i= 0:(4) Si toutes les variablesx1;x2;:::;xnsont independantes, cette condition est veriee pour @f@x i= 0; i= 1;2;;n:(5) Si les variablesxiverient une contrainte supplementaire sous la forme (contrainte de type holonome) 6 g(x1;x2;;xn) =C;(6)6. Du grec \holos" qui signie \la totalite" et \nomos", la loi. 10 ouCest une constante, les variablesxine sont plus independantes et l'extremum de la fonction n'est plus obtenu par lesnequations (5). Il faut tenir compte de cette contrainte et exprimer, par exemple,xnen fonction dex1,x2,...,xn1et remplacerxndans l'expression def. On se ramene donc a un probleme an1 variables independantes avecn1 equations (5) pouri= 1;2;:::;n1...ce qui peut ^etre tres complique! Une alternative ecace est d'introduire une nouvelle variable, qui sera calculee a posteriori (l'ajout d'une variable pour lever une contrainte est assez courant en physique). Voyons deux facons dierentes d'introduire cette methode dite des \multiplicateurs de

Lagrange" :

i)Rechercher l'extremum de la fonctionf(x1;x2;:::xn) anvariables avec la contrainte (6) est equivalent a rechercher l'extremum de la fonctionF(x1;x2;:::;xn;) an+1 variables sans contrainte

F(x1;x2;:::;xn;) =f(x1;x2;:::;xn)

g(x1;x2;;xn)C |{z} =0; ouest un reel a determiner ulterieurement, appele \multiplicateur de Lagrange". Les n+ 1 variables etant independantes l'extremum est donne par @F@x i=@f@x i@g@x i= 0;pouri= 1;2;;n: et @F@ =Cg(x1;x2;;xn) = 0; soit l'expression de la contrainte (6). Lesnpremieres equations permettent ainsi d'expri- mer lesxien fonction du multiplicateur de Lagrangequi est ensuite calcule a l'aide de la contrainte (6). ii)Adoptons un point de vue geometrique. Au cours d'une promenade en montagne, on cherche le point le plus eleve. Icif(x;y) est l'altitude du point de coordonnees (x;y) et g(x;y) =Cdenit la trajectoire du promeneur qui est imposee. Figure5 {La fonctionf(x;y)est l'altitude du point de coordonnees(x;y)(sur une carte) et le chemin parcouru d'equationg(x;y) =C(en rouge) est impose. Les lignes de niveauf(x;y) =ctesont representees en bleu. Aux points ou le chemin coupe une ligne de niveau (f(x;y) =cte), le chemin est en pente. Un extremum (stationnaire) correspond forcement a un point ou le chemin est 11 tangent a une ligne de niveau. Autrement dit, au point extremal les vecteurs gradients sont colineaires : rf=r(gC); ouest le multiplicateur de Lagrange. On retrouve @f@x @g@x = 0 @f@y @g@y = 0: Illustrons la methode des multiplicateurs de Lagrange par deux exemples :

Supposons que la montagne a un prol parabolodal :

f(x;y) = 1x2y2; tel que son sommet est enx=y= 0 a l'altitudef(0;0) = 1. La projection du chemin dans le plan (x;y) a pour equationg(x;y) =y+x=12 . Le point du chemin dont l'altitude est la plus elevee est donc donne par le maximum de

F(x;y) = 1x2y2y+x12

Soit @F@x =2x= 0;@F@y =2y= 0 et@F@ =y+x12 = 0: Le chemin passe donc par un point d'altitude maximale 7=8 enx=y==2 = 1=4. Reprenons l'exemple de la bo^te cylindrique. Introduisons le multiplicateur de La- grange. On cherche les extrema de

F(L;R;) =S(L;R)(V(L;R)V0):

Soit @F@L =@S@L @V@L = 2RR2= 0; @F@R =@S@R @V@R = 4R+ 2L2RL= 0: Donc

R= 2=;

L= 4=:

On en deduita l'aide de la contrainte :V0=R2L= 16=3donc= (16=V0)1=3.

Finalement, on retrouveR=L2

= (V0=2)1=3.quotesdbs_dbs22.pdfusesText_28

[PDF] identité de beltrami

[PDF] probleme variationnel lagrangien

[PDF] formulation variationnelle exercices corrigés

[PDF] cours volume 6ème

[PDF] comment calculer le déterminant dune matrice 4x4

[PDF] determinant matrice inversible

[PDF] determinant matrice exercices corrigés

[PDF] determinant matrice 2x3

[PDF] calcul du determinant dune matrice pdf

[PDF] déterminant matrice triangulaire

[PDF] forme canonique de commandabilité

[PDF] représentation d'état exercices corrigés pdf

[PDF] passage fonction de transfert représentation d'état

[PDF] forme modale automatique

[PDF] forme compagne de commande