[PDF] Caractéristiques des distributions à un caractère

View - Download Caractéristiques des distributions à un caractère

Previous PDF

Next PDF

Caractéristiques des distributions à un caractère

1 LES CARACTÉRISTIQUES DE LA TENDANCE CENTRALE

Il est souvent utile de réduire les données ou de les résumer par le calcul de paramètres ou de va-

leurs typiques qui permettent de caractériser de façon simple les séries statistiques et les distributions

observées. Nous allons nous intéresser à trois types de paramètres :paramètres de position (tendance

centrale), paramètre de dispersion, paramètres de disymétrie.

1 Les caractéristiques de la tendance centrale

Elles servent à caractériser l'ordre de grandeur des observations.

1.1 Le mode

On appelle mode(s) (ou valeur(s) dominante(s) d'une distribution discrète )(données non regroupées)

la ou les valeurs(s) observée(s) de fréquences (ou d'effectif) maximum. De même, on appelle classe

modale d'une distriburtion continue (données regroupées) la ou les classe(s) de fréquences maximum.

Si les classes ne sont pas de même amplitude on définit la classe modale comme étant celle qui a une

densité de fréquences maximum. Remarque :Une distribution est diteunimodalesi elle admet un mode unique,bimodalesi elle admet deux modes ouplurimodalesi elle admet plusieurs modes.

Exemples :

1.Variable discrète

Il est possible de déterminer le mode aussi bien pour des variables qualitatives que quantitatives.

Reprenons le tableau des données présenté dans la précédente séance :

Département de naissance(xi)Effectifs(ni)

055
0618
7580
7764
9170
Tab.1 - Département de naissance des femmes hospitalisées dans un hopital parisien Le département75presente le plus grand nombre de femmes hospitalisées dans cet hopital (80).

C"est le mode de cette distribution.

2.Variable continueIl faut distinguer le cas ou les classes sont de même amplitude et le cas ou elles ne

le sont pas. 2

1.1 Le mode

•Classes de même amplitude

AgesCiEffectifs(ni)fréquencesfi

C1:[10,15[1010/80

C2:[15,20[1818 /80

C3:[20,25[1515/80

C4:[25,30[3030/80

C5:[30,35[77/80

Tab.2 - Distribution de l"âge des clients rentrant dans un magasin de musique

La classe modale estC4:

[25,30[ , c"est elle qui présente le plus fort effectif ou la plus forte fréquencre. •Classes d"amplitudes différentes

La détermination de la classe modale se fait à partir de la densité des fréquenceshi. D"autres

moyens qui tiennent compte des amplitudes des classes peuvent être utilisés. AgesCiEffectifs(ni)Fréquences relatives(fi)Densité de fréquences(hi)

C1:[10,15[1010/8010/400

C2:[15,25[1818/8018/800

C3:[25,30[1515/8015/400

C4:[30,50[3030/8030/1600

C5:[50,55[77/807/400

Tab.3 - Distribution des salaires des employés d"une entreprise La plus forte densité de fréquences est15/400, la classe correspondanteC3: [25,30[est la classe modale. Remarque :Dans le cas d"une distribution continue, il est possible de determiner graphiquement un mode dans la classe modale :

Mo=L+ai?Δi

Δi+ Δs?

oùL: représente la borne inférieure de la classe modale, a i: l"amplitude de la classe modale,i

Δi:l'excéden

t d'effectif ou de fréquence entre la classe modale et la classe pré-modale,

Δs:l'excéden

t d'effectif ou de fréquence entre la classe modale et la classe post-modale .Remarque: si les amplitudes entre la classe modale et les classes adjac entes sont différentes, on calcule les excédents de densités de fréquence au lieu des exceédents de fréquences ou d'effectifs. 3

1 LES CARACTÉRISTIQUES DE LA TENDANCE CENTRALE

Fig.1 - Détermination graphique de la valeur du mode. La figure représentela portion d"un histo-

gramme entourant la classe modale.

1.2 Les moyennes

Il existe plusieurs manières de calculer une valeur moyenne suivant sa signification. Nous nous focalisons

dans ce cours sur les moyennes classiques.

1.2.1 La moyenne d"ordre 1 ou la moyenne arithmétique

La moyenne arithmétique d'une série de données x

1,...,xi,...xn, ou tout simplement la moyenne, notée

x, est égale à la somme des valeurs obsevées divisée par le nombre n d'observations, soit :

x=1nn i=1x i

Comme chaque valeur x

idoit être prise en considération, le cas échéant autant de fois qu'elle a été observée, cette expression devient alors : x=1nk i=1x i=k? i=1n inxi=k? i=1f ixi

Pour obtenir la moyenne d'une distribution continue (ou de données groupées), on remplace, dans les

expressions suivantes, lesxipar les centres des classesci.

Propriétés :

?k i=1(nixi- x ) = 0

Preuve :

?k i=1(nixi- x ) =?k i=1nixi-nx=nx-nx= 0 4

1.3 Les quantiles

•y=ax+b

siaetbdésignent deux constantes telles que pour toutes les valeurs observées ou tous les centres

de classesxion ayi=axi+b.

Preuve :

y=1n? k i=1niyi=1n? k i=1ni(axi+b) =1n(a?ki=1nixi+nb) =ax+b •La fonctiong(a) =?k i=1ni(xi-a)2est minimale ena= x Preuve :il suffit de résoudre l"équationg?(a) = 0. (xq1,....,xqi,...,xqkq)qséries statistiques

d"effectifs différents (mais de même nature), la moyenne générale est obtenue comme suit :

x=? q j=1? kj i=1xji?q j=1kj=? qj=1(kjxj)?qj=1kj, C"est la moyenne arithmétique pondérée des différentes moyennes xj, les coefficients de pondé- ration étant les effectifskjdes différentes séries statistiques.

1.2.2 La moyenne d"ordrer

La moyennequadratiqueoud"ordre 2d"une série de donnéesx1,...,xi,...xnest la racine des moyennes

des carrés, soit : x2=? ???1 nn i=1x 2i( 1 nn i=1n ix2i)

Cette moyenne est utilisé

een thermodynamique où l"on montre que la température absolue d"un gaz est liée aux carrés des vitesses des molécules de ce gaz.

Plus généralement, on définitla moyenne d"ordre roude degré kde la suite de donnéesx1,...,xi,...xn

par : xr=? 1nn i=1x ri? 1/r( 1nk i=1n ixri? 1/r)

Exemple :

Si un rectangle a pour côtés3et7, le carré qui a même diagonale que le rectangle a pour côté la

moyenne quadratique de3et7, c"est à dire5.38.

1.3 Les quantiles

1.3.1 la médiane

La médiane est la valeur de la variable (ou du caractère) qui se situe aucentre de la série statistique

simple classée par ordre croissant (ou décroissant). C"est une valeur qui sépare la distribution en deux

5

1 LES CARACTÉRISTIQUES DE LA TENDANCE CENTRALE

groupes d"égale importance numérique. Ainsi50%des éléments de l"échantillon ont une valeure infé-

rieure à la médiane et50%une valeur supérieure.

•Dans le cas d"un caractère discret on notex(1),...,x(i),...x(n), la médiane est définiepar

-Mé=x((n+1)/2), sinest impair, -[x(n/2),x(n/2+1)]est un intervalle median. Un choix possible d"une médiane dans cet intervalle est donné parMé=x(n/2)+x(n/2+1) 2.

•Dans la cas continu (ou données groupées), il faut considérer les effectifs ou les fréquences cumulés

et procéder par interpolation linéaire. Soit [ bi,bi+1[la classe des données pour

laquelle les effectifs cumulés (ou les fréquences cumulées) atteignentn/2éléments de l"échantillon

( ou1/2). On suppose que les éléments de cette classe sont uniformément répartis à l"intérieur

de celle-ci, la médiane est alors obtenue par :

Mé=bi+(bi+1-bi)?

n/

2)-Ni-1 ni?

Mé=bi+ (bi+1-bi)?(1/2)-Fi-1

f i

Remarque :

A partir de la fonctionFdes fréquences cumulées, on définit la médiane comme suit : Mé=F-1(1/2), F-1étant l"inverse généralisée deF

Exemples :

1. SoitS={1,7,8,3,6,12,20,19,18}une série de notes obtenues par un élève. La série ordonnée

des notes estS()={1,3,6,7,8,12,18,19,20}, la médiane estMé= 8. Si on considère la série S ?= 1,7,3,6,12,20,19,18,S?()={1,3,6,7,12,18,19,20}, l"intervalle médian est alors[7,12]et une médianeMé=(7+12)/2=9,5

2. Reprenons les données du tableau Tab 2, rajoutons la colonne relative aux fréquences cumulées,

on obtient le tableau suivant AgesCiEffectifs(ni)fréquencesfifréquences cumuléesFi

C1:[10,15[1010/8010/80

C2:[15,20[1818 /8028/80

C3:[20,25[1515/8043/80

C4:[25,30[3030/8073/80

C5:[30,35[77/8080/80

Tab.4 - Distribution de l"âge des clients rentrant dans un magasin de musique

La médiane appartient donc à la classeC3,M?[20,25[. En utilisant ce qui précède, on obtient

M= 20 + (25-20)?40-28

15? = 24

1.3.2 Généralisation aux quantiles

Soitα?]0,1[, le quantile d"ordreα(ou leα-quantile) est la valeur du caractèreqαqui vérifie :

6

1.l'ensem ble des individus dont le caractère est au plus égal àqαest de[nα]+1, où [[.]représente la

partie entière denα, ou na si c'est un nombre entier, 2. l'ensem ble des individus dont le caractère est au moins égal àqαest den-[nα].

Quelques quantiles particuliers :

•Les pourcentiles :α? {0.01,0.02,...,0.99} •Les déciles :α? {0.1,0.2,...,0.9} •Les quartiles :α? {0.25,0.5,0.75}

Remarque :

A partir de la fonctionFdes fréquences cumulées, on définit le quantile d"ordreαcomme suit :

q

α=F-1(α)

Le calcul des différents quantiles est analogue à celui de la médiane.

Exemple :

Reprenons le tableau Tab 4 puis cherchons, par interpolation linéaire, les différents quartilesQ1,Q2et

Q 3 •Q1=q0.25= 17.77 •Q2=q0.5=Mé= 24 •Q3=q0.75= 27.83

2 Caractéristiques de dispersion ou variabilité

Les paramètres de dispersion nous renseignent sur l'étalement de la distribution. En e ff et, deux distri-

butions de fréquences peuvent avoir la même moyenne, la même médiane et le même mode et présenter

des formes très di ff érentes. Les caractéristiques (ou paramètres) les plus utilisés sont l'écart interquartiles, la variance et l'écart-type.

2.1 L"étendue

L'étendue est la di

ff érence entre les valeurs extrêmes de la distribution (la plus grande et la plus petite valeur de la variable). Ce paramètre, notéEest rarement utilisé,

E=maximum-minimum=x(n)-x(1)

Exemple :

Soit la série des données suivanteS={10,1,5,7,2,20},x(6)= 20etx(1)= 1,E= 20-1 = 19.

2.2 L"écart interquartile

C'est la différenceI = Q3 - Q1. Cet intervalle englobe la moitié, ou approximativement la moitié, des

observations qui se situent au centre de la distribution. Ce paramètre, est assez souvent utilisé.

Exemple :

Soit la série des données suivanteS={3,4,5,2,1,10,16,13,7,29,21},Q3= 14.5etQ1= 3.5,I= 14

5-3.5 = 11.

7

2 CARACTÉRISTIQUES DE DISPERSION OU VARIABILITÉ

2.3 La variance

Au niveau de la population statistique, la variance est la moyenne arithmétique des carrés des écarts

des valeurs à leur moyenne, var(x) =1 nk i=1n i(xi-x)2=k? i=1f i(xi-x)2=1nk i=1n ixi2-x2=k? i=1f ixi2-x2 Pour les variables continues,xireprésentent les centres de classes. Remarque :On notera aussi que de nombreux auteurs définissent la variance en divisant la somme

des carrés des écarts par rapport à la moyennen-1, et non pasn. De même, de nombreux logiciels

effectuent le calcul de la variance de cette manière.

2.3.1 L"écart-type

C'est la racine carrée de la variance, aussi appeléécart quadratique moyenoud viation standard var(x)

Cette quantité représente l'avantage de s'exprimer en même unité que la variable et donne une idée

plus précise de la ßuctuation autour de la moyenne. Exemple :Longueur du corps de 20 vaches laitières. Pour un lot de 20 vaches, les observations sont, en centimètres :

145, 146, 148, 150, 150,151, 151, 154, 155, 157, 158, 159, 161, 161, 163, 165,168, 169, 169, 176.

x=120(145 +...+ 176) = 157.8

V(X) =1

20((145-157.8)2+ (146-157.8)2+...+ (176-157.8)2) = 71.16

71

16 = 8

4 4 Remarque :On suppose que la population statistique est composée de plusieurs sous-populations P

1,P2,...,Pk).C"est le cas d"une entreprisePcomposée de plusieurs établissementsP1,P2,...Pk. On

suppose que les salaires moyens dans ces établissements sont x1,x2,...,xk, le salaire moyen de l"entre- prisePest x=1n(n1x1+n2x2+...+nkxk). La variance est donnée par l"expression suivante : var(x) =1 n(n1var(x1) +n2var(x2) +...+nkvar(xk)) +1n(n1(x1-x)2+...+nk(xk-x)2) 1 nk i=1n ivar(xi) +1nk i=1n i(xi-x)2 var(xi) +var(xi), où 8

2.4 Les moments d"ordrer

-var(xi),variance intrapopulation, est la variance que l"on obtiendrait si toutes les sous-populations

avaient la même moyenne (moyenne globale), -var( xi),variance interpopulation, est la variance que l"on obtiendrait si les sous populations

étaient homogènes c.a.d. chaque variable de chaque sous populationétait égale à sa moyenne.

2.4 Les moments d"ordrer

Le moment d'ordre 2 n'est autre que la variance. De manière générale, on définit le moment d'ordre r,

notéµrde la façon suivante : r= xr=1nk i=1n i(xi-x)r Ces moments seront utiles dans les sections suivantes.

2.5 Autres caractéristiques de dispersion

Les caractéristiques suivantes sont rarement utilisées :

1. Ecart absolu moyen par rapport à la moyenne ar

i thmétique eX=1nk i=1n i|x i-x|

2. Ecart absolu par rapport à la médiane

eM=1nk i=1n i|xi-M|

3. Intervalle interdécile

I

D=D9-D1

4. Coefficient de variation : dans certaines situations, on désire comparer le taux de dispersion de

distributions alors que leur échelle de mesure respective ne sont pascomparables, l"objectif de ce

coefficient est de fournir un indice quantitatif permettant cette comparaison car il est sans unité

C.V.=σ

x×100%

L'étendue

, l'intervalle interquartile, l'écart absolu moyen et l'écart type sont des paramètres de dispersion

absolue qui mesurent la variation absolue des données.

Ils s'expriment dans l'unité de mesure de la

variable.

3 Caractéristiques de forme

3.1 Mesure de l"asymétrie

Les courbes suivantes (Figure 2) donnent une idée sur la forme d'une distribution quelconque : Distri

bution

symétrique, distribution non symétrique (courbe oblique à gauche), distribution non symétrique

(courbe oblique à droite). 9

3 CARACTÉRISTIQUES DE FORME

Fig.2 - Mesures de l"asymétrie. Centre : Distribution symétrique. Gauche et droite : Distributions

non symétriques

Certains coefficients (indices) permettent de situer la distribution dans un des trois cas précédents :

1.Coefficient de Yule

S=(Q3-M)-(M-Q1)

(Q3-M) + (M-Q1)? ?S= 0symétrie

S >0la courbe est étalée à droite

S <0la courbe est étalée à gauche

2.Coefficient de Pearson

S 1= x-M0 ?S

1= 0symétrie

S

1>0la courbe est étalée à droite

S

1<0la courbe est étalée à gauche

3.Coefficient de Fisher

1=μ3

σ3?

1= 0symétrie

1>0la courbe est étalée à droite

1<0la courbe est étalée à gauche

3.2 Mesure de l"aplatissement

La courbe normale (mesokurtique du latin kurtosis) est celle qui représente une série de données issues

d'une distribution suivant une loi normale. Un courbe est aplatie (platykurtique du latin plutos (large))

quand une variation forte de la valeur étudiée ne s'accompagne pas de forte variation de la fréquence,

par référence à la courbe des fréquences de la loi normale. Une courbe est concentrée (leptokurtique

du latin leptos (mince)) si elle est moins aplatie que la distribution normale (Figure 3). 10

3.2 Mesure de l"aplatissement

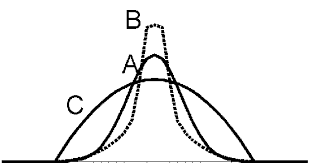
Fig.3 - Mesures de l"aplatissement. Courbe A : Distribution normale. Courbe B : Distribution lepto- kurtique. Courbe C : Distribution platykurtique. La mesure de l"aplatissement peut s"effectuer par l"intermédiaire des coefficients suivants :

1.Coefficient de Pearson

2=μ4

μ22=μ4σ4???β

2= 3courbe normale

2>3courbe leptokurtique

2<3courbe platykurtique

2.Coefficient de Fisher

2=β2-3 =μ4

σ4-3???γ

2= 0courbe normale

2>0courbe leptokurtique

2<0courbe platykurtique

11quotesdbs_dbs15.pdfusesText_21

[PDF] série statistique discrète et continue

[PDF] formule pib optique demande

[PDF] pib = cf + fbcf + vs + xm

[PDF] pib optique revenu

[PDF] comment calculer le pouvoir d'achat formule

[PDF] exemple de calcul du pouvoir d'achat

[PDF] calcul indice prix consommation

[PDF] calcul pouvoir d'achat ses

[PDF] calcul du pouvoir d'achat du revenu disponible brut

[PDF] compte de résultat syscoa excel

[PDF] compte de résultat cours

[PDF] calcul du seuil de pauvreté 2017

[PDF] la pauvrete causes consequences et solutions

[PDF] taux de pauvreté formule

[PDF] calcul du seuil de pauvreté 2016