 1. Mode - Classe modale 2. Médiane - Classe médiane
1. Mode - Classe modale 2. Médiane - Classe médiane
Une série statistique peut avoir plusieurs modes ou classes modales. Le mode ou la classe modale désigne l'endroit ùla répartilion est la plus dense et
 statistiques corrigé
statistiques corrigé
Une classe modale est une classe pour laquelle l'effectif est le plus élevé. :::::::::: Exercice 6 :::::::::::::::::::: 1. Quel est le mode de la série A
 Cours dintroduction 0pt40pt à lanalyse statistique 0pt30pt 3
Cours dintroduction 0pt40pt à lanalyse statistique 0pt30pt 3
Détermination graphique du mode d'une classe modale. Si on ne suppose pas que Exemple : La classe médiane de revenus est la classe ]100200]. En supposant ...
 â /-/../frft-5 6a
â /-/../frft-5 6a
Effectif de la classe après la classe modale. rcffife : Soit le tableau süvant qui représenle !a répartition. :flr#*
 Séance 4
Séance 4
Dans une distribution connue par classes ou catégories: - Si le caractère est quantitatif continu la classe modale est celle de plus grande densité de
 TYPOLOGIE DES CLASSES MODALES
TYPOLOGIE DES CLASSES MODALES
(1) En tempérament égal le rapport de fréquences correspondant à un intervalle élémentaire sur une trame de résolu- tion ρ vaut 21/r.
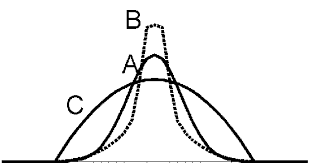 Caractéristiques des distributions à un caractère
Caractéristiques des distributions à un caractère
Si les classes ne sont pas de même amplitude on définit la classe modale comme étant celle qui a une densité de fréquences maximum. Remarque : Une distribution
 TITRE 1
TITRE 1
Attention : Si on fait des regroupements en classes la classe modale dépend du découpage retenu. Dans l'exemple 2 la classe modale est [1000 ; 1500[ par contre
 Statistiques
Statistiques
11 avr. 2018 La classe qui a le plus grand effectif est appelée classe modale. REMARQUE : il peut y avoir plusieurs modes et plusieurs classes modales.
 Chapitre 2: Les caractéristiques de tendances centrales
Chapitre 2: Les caractéristiques de tendances centrales
On appelle classe modale une classe dont la fréquence moyenne par unité de on s'intéresse uniquement `a trois classes : la classe modale et les deux classes ...
 1. Mode - Classe modale 2. Médiane - Classe médiane
1. Mode - Classe modale 2. Médiane - Classe médiane
Une série statistique peut avoir plusieurs modes ou classes modales. Le mode ou la classe modale désigne l'endroit ùla répartilion est la plus dense et
 statistiques corrigé
statistiques corrigé
Calculer la fréquence d'une valeur ou d'une classe : Une classe modale est une classe pour laquelle l'effectif est le plus élevé.
 Séance 10
Séance 10
Pour l'Alsace calculer : a. le salaire moyen
 Séance 4
Séance 4
Ou nj = l'effectif de la classe cj = le centre de la classe Si le caractère est quantitatif continu la classe modale est celle de plus grande densité.
 1 Leffectif dune classe statistique est le nombre déléments de la
1 Leffectif dune classe statistique est le nombre déléments de la
tranche de 500€ la classe modale serait [500 ; 1000[. LA MEDIANE. La médiane d'une série statistique est une valeur de la variable telle qu'il y ait.
 Cours de statistique descriptive - Archive ouverte HAL
Cours de statistique descriptive - Archive ouverte HAL
2 août 2016 intervalle ces valeurs peuvent alors être regroupées en classes
 TITRE 1
TITRE 1
tranche de 500€ la classe modale serait [500 ; 1000[. LA MEDIANE. La médiane d'une série statistique est une valeur de la variable telle qu'il y ait autant.
 Caractéristiques des distributions à un caractère
Caractéristiques des distributions à un caractère
La classe modale est C4 :[25 30[
 STATISTIQUE DESCRIPTIVE
STATISTIQUE DESCRIPTIVE
Dans le cas d'une variable statistique continue on parle plutôt de classe modale. NB : Le mode ou la classe modale n'est pas obligatoirement unique.
 VARIABLES QUANTITATIVES CONTINUES
VARIABLES QUANTITATIVES CONTINUES
(c) Déterminer la classe modale de la variable. (d) Représenter graphiquement la proportion de salariés ayant un trajet compris entre 7 et 22 minutes.
 [PDF] 1 Mode - Classe modale 2 Médiane
[PDF] 1 Mode - Classe modale 2 Médiane
Une série statistique peut avoir plusieurs modes ou classes modales Le mode ou la classe modale désigne l'endroit ùla répartilion est la plus dense et
 [PDF] Les paramètres statistiques de centralité
[PDF] Les paramètres statistiques de centralité
Dans une distribution connue par classes ou catégories: - Si le caractère est quantitatif continu la classe modale est celle de plus grande densité
 [PDF] Cours de statistique descriptive
[PDF] Cours de statistique descriptive
Le mode est alors le centre de la classe modale c'est à dire la classe qui a la fréquence moyenne la plus élevée Page
 Moyenne Médiane Classe Modale Et Dispersion DUne Série
Moyenne Médiane Classe Modale Et Dispersion DUne Série
Moyenne Médiane Classe Modale Et Dispersion D'Une Série Statistique Téléchargez comme PDF TXT ou lisez en ligne sur Scribd
 [PDF] Chapitre-3pdf - UMMTO
[PDF] Chapitre-3pdf - UMMTO
a- Déterminer la classe modale : Ciest la classe qui a le plus grand effectif ou la plus granCe f iiffiJiliTi; rormure :Mo: ito * ai (hiwo * ni no
 [PDF] Séries Statistiques Simples - EcoFoG
[PDF] Séries Statistiques Simples - EcoFoG
2 2 Mode Classe modale 2 3 Effectifs Fréquences cumulées 2 4 Médianes 2 5 Variance Ecart-Type 2 6 Caractéristiques de position
 [PDF] 1 Chapitre 03 : Etude dune variable statistique continue
[PDF] 1 Chapitre 03 : Etude dune variable statistique continue
Definition 8 Nous définissions la classe modale comme étant la classe des valeurs de X qui a le plus grand effectif partiel (où la plus grande fréquence
 [PDF] STATISTIQUE DESCRIPTIVE
[PDF] STATISTIQUE DESCRIPTIVE
Dans le cas d'une variable statistique continue on parle plutôt de classe modale NB : Le mode ou la classe modale n'est pas obligatoirement unique
 443 Calcul du mode - Statistique Canada
443 Calcul du mode - Statistique Canada
2 sept 2021 · La classe modale serait l'intervalle de 160 à 179 cm car c'est celle avec la fréquence la plus élevée Tableau 4 4 3 5 Nombre de personnes
C'est quoi la classe modale ?
Le mode, ou la classe modale, est une mesure de tendance centrale qui permet de rapidement analyser la donnée, ou le groupe de données, la plus populaire d'une distribution. Le mode (Mod) est la valeur dont l'effectif est le plus élevé dans une distribution de données.Comment déterminer la classe modale ?
Pour calculer le mode d'une distribution de données groupées, on peut utiliser le milieu de l'étendue (ou de l'amplitude) de la classe modale.
1LMod=48.2d1=9.3d2=12.4a=3.Quel est la formule de mode ?
Mode : La valeur la plus fréquente d'une série statistique — C'est la (ou les) valeur(s) du caractère dont l'effectif est le plus grand. Exemple : le mode de la série {4 , 2, 4, 3, 2, 2} est 2 car il apparaît trois fois. 2 est la valeur qui a le plus grand nombre d'occurrences.- La formule de sturge k =1+3.3 log10 (N) . La formule de yule k = 2.5 4 ?N. Remarque :On peut avoir plusieurs tableaux statistiques selon le nombre de classes.
1 Chapitre 03 : Etude d"une variable statistique
continue On appelle V.S continue (ou caractère continu) toute application de et à valeurs réelles et qui prend un nombre "important" de valeurs (Les caractères continus sont ceux qui ont une in...nité de modalités).Question :Comment étudier ce caractère ?
Réponse: Partager les valeurs prises parXen classes de valeurs.1.1 Classe de valeurs
De...nition 1On appelle classe de valeurs deXun intervalle de type[a;b[tel queX2[a;b[si et seulement siaX(w)< b, c"est à dire, que les valeurs du caractère sont dans la classe[a;b[. Dès qu"un caractère est identi...é en tant que continu, ces modalitésCk= [Lk;Lk+1[sont des intervalles avec1.Lk: borne inférieure,Lk+1: borne supérieure.
2.L"amplitudede classeknotéeakdonnée par :
a k=Lk+1Lk3.Le centrede classeknotéeCkdonnée par :
C k=Lk+Lk+12 dans ce chapitre trois formules suivant : pN;[pN] (partie entière)ou[pN] + 1. Donc, le nombre de classes k'pN:La formule de sturge
k= 1 + 3:3log10(N):La formule de yule
k= 2:54pN: Remarque :On peut avoir plusieurs tableaux statistiques selon le nombre de classes. 1De...nition 2La quantité
n i=Cardf!2 :X(!)2Cig: Nombre d"individus qui prennent des valeursxidansCi:De...nition 3Le nombre
f i=niN est appelé la fréquence partielle deCi: N i=iX j=1n j: De...nition 5On appelle la fréquence cumulé duCila quantité F i=iX j=1f j:1.3 Répresentation graphique d"un caractère quantitatif
continue : Comme dans le cas dans variable statistique discret la répresentation graphique d"un caractère quantitatif continue se presente sous deux formes (diagrammeExample 6Tableau statistique :
2Les classesn
if ia iC id i=nia iN iFTotal2001
1.3.1 Répresentation graphique : (Histogramme)
A chaque classe est associée un rectangledont la longeur est l"amplitude de la classe et dont la hauteur estnia ioùfia i:1.3.2 Fonction de répartition
De...nition 7La fonctionFx:R![0;1]dé...nie parFx(x)représenter le pour- centage des individus tel que la valeur de leur caractère est inférieure ou égaleàx:Elle est donnée par
F x(x) =8 >>>:0sixxmin F1sixminxxmin+1
F isixixxi+11sixxn
et elle s"appelle la fonction de répartition deX: 3 Nous expliquons cette formulation de la fonction de répartitionn dans cette remarque . La courbe deFxest nulle avanta0, constant égale à 1 aprésanet joint les points(a0;0);(a1;F1):::::(an;1)par des segments de droites.La courbe des fréquences cumulées.
1.3.3 Caractéristique de position centrales :
On noteCile centre de classeCiet nous considéronsfila fréquence partielle.1.La moyenne arithmétique :
x=1N m X i=1n iCi=mX i=1f iCi: (2)Le mode: La dé...nition suivante permet de comprendre la démarche à suivre pour calculer le mode d"une manière exacte et qui se trouve dans une des classes appelée "classe modale". De...nition 8Nous dé...nissions la classe modale comme étant la classe des valeurs deXqui a le plusDans l"example5
La classe modale est[400;600[dans ce cas on peut prendre M o=400 + 6002 = 500: 4 On peut aussi déterminer graphyquement le mode : La quantité M o=Li1+ai1 1+ 2Tel que :
Li1:La borne inférieur de la classe modale.
ai:Le pas de classe modale.1=n0n1;2=n0n2où bien1=f0f1;2=f0f2:
modale. Représentation ou détermination graphique du mode (cascontinu).Dans l"example5:
M o= 400 + 2000:3000:225(0:3000:225) + (03000:285)'567 (2)La médianeMe:C"est la valeurMetel queF(Me) = 0:5oùFest la fonction cumulative la classe[Li1;Li[: Nous pouvons la déterminer graphiquement où par calcule:Graphiquement à partir de la formule
5 tan=F(Li+1)F(Li)L i+1Li=F(Me)F(Li)M eLi=0:5F(Li)M eLi Plus précisément, dans la ...gure ci-dessous, nous mettonsF(x) = 0:5et x=Me.Dans l"example 5:Me2[400;600[
M e= 400 + 2000:50:2250:5250:2255842[400;600[:1.3.4 Caractéristique de dispersion :
(a)L"étendu: Le nombreE=emaxemin:
S"appelle étendu deX.
Example 5:E= 1200200 = 1000
(b)La Variance: est la quantitéV ar(X) =1N
m X i=1n iciX2=mX i=1f iciX2: (c)L"écart typex:est la quantité 6 x=pV ar(X) =v uutm X i=1f iciX2: (d)L"écart absolue moyen : E ab=1N m X i=1n iciX Nous généralisons la notion de la médiane dans la dé...nition suivante. (e)Les quartiles :Pouri2 f1:2:3g;la quantitéQitel queF(Qi) =i4
s"appelleiemequartile.Pouri= 2; Q2telqueF(Q2) =24
= 0:5:DoncQ2=Me: Interprétation: Il y a25%d"individus dont la valeur du caractère est dans l"intervalle[a0;Q1]. De même pour les autres quartiles. Ces intervalles s"appellent "intervalles interquartiles". Q1!25%;
Q2!50%;
Q3!75%:
Les quartiles.
7quotesdbs_dbs15.pdfusesText_21[PDF] formule pib optique demande
[PDF] pib = cf + fbcf + vs + xm
[PDF] pib optique revenu
[PDF] comment calculer le pouvoir d'achat formule
[PDF] exemple de calcul du pouvoir d'achat
[PDF] calcul indice prix consommation
[PDF] calcul pouvoir d'achat ses
[PDF] calcul du pouvoir d'achat du revenu disponible brut
[PDF] compte de résultat syscoa excel
[PDF] compte de résultat cours
[PDF] calcul du seuil de pauvreté 2017
[PDF] la pauvrete causes consequences et solutions
[PDF] taux de pauvreté formule
[PDF] calcul du seuil de pauvreté 2016
