 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Or arccos(x) ∈]0π[ et sin(arccos(x)) > 0. Donc sin(arccos(x)) = √1 - x2 1 Représentez la fonction x ↦→ arcsin(sin(x)). 2 Représentez la fonction x ...
 Chapitre12 : Fonctions circulaires réciproques
Chapitre12 : Fonctions circulaires réciproques
D'où comme pour Arcsin
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
f3(x) = arcsin√1−x2 −arctan. (√. 1−x. 1+x. ) . 4. f4(x) = arctan 1. 2x2 −π +2kπ ⩽ x < 2kπ alors arccos(cosx) = arccos(cos(2kπ −x)) = 2kπ −x avec k ...
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
tan(x) = y ⇐⇒ x = arctan y arctan (x) = 1. 1 + x2. ∀x ∈. Mini-exercices. 1. Calculer les valeurs de arccos et arcsin en 0 1
 Cours3 Compléments trigonométrie
Cours3 Compléments trigonométrie
sin(Arcsin( )) cos(Arcsin( )) Si deux nombres sont égaux alors ils ont la même tangente (mais la réciproque est fausse) donc… SI Arctan( ) Arctan(4) Arctan(5).
 1) La fonction Arccos.
1) La fonction Arccos.
Par le cours on en déduit que sa fonction réciproque Arccos est dérivable exemple Arctan(tan(3π)) = Arctan(0) = 0. Question : si x est un réel tel que x ...
 I Propriétés fondamentales
I Propriétés fondamentales
Groupe-cours 51. MAT1112 - Calcul Le graphe de f−1 est le symétrique du graphe de f par rapport à la droite y = x. III.2 Les fonctions arccos arcsin
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
arccosarcsin
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Chapitre12 : Fonctions circulaires réciproques
Chapitre12 : Fonctions circulaires réciproques
4.0 International ». https://www.immae.eu/cours/. Chapitre12 : Fonctions circulaires D'où comme pour Arcsin
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Cours magistral 4 : Réciproques des fonctions trigonométriques sin(arccos(x))? Ce que l'on sait cos(arccos(x)) = x et ... arcsin(sin(x)) = x Vx ? [-?.
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
ter à notre catalogue de nouvelles fonctions : chsh
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
de nouvelles fonctions : ch sh
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 2.5.4 Compléments (fonctions trigonométriques inverses)
2.5.4 Compléments (fonctions trigonométriques inverses)
arcsin(x)+arccos(x)= y + arcos(cos( ?. 2. ? y)) = ?. 2 . III. La fonction arctan: la fonction tangente est monotone (strictement croissante) sur
 TD 1 Intégrales généralisées
TD 1 Intégrales généralisées
16 sept. 2016 Résumé de cours. 2. Exercices. ... Arctan etc) n'ont pas toujours de primitives élémentaires. ... Arcsin d – Arcsin c
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
I : Incontournable T : pour travailler et mémoriser le cours 3. f3(x) = arcsin?1?x2 ?arctan ... 2sinxcosx(arcsin(
 Résumé des propriétés des fonctions trigonométriques
Résumé des propriétés des fonctions trigonométriques
réciproques arcsin arccos et arctan. Résumé de cours sur les nombres complexes. Le nombre imaginaire i est introduit comme solution de x2 = ?1 et vérifie
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
cours du mercredi 1/3/17 Chapitre V Fonctions arcsin arccos arctan 1 Définitions 1 1 arcsin Proposition 1 1 La fonction sin : [??/2 ?/2] ? [?11]
 [PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
[PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
décroissante donc est une bijection Sa bijection réciproque est la fonction arccosinus : { cos(x) = y x ? [0?] ? { x = arccos(y) y ? [-11]
 [PDF] 254 Compléments (fonctions trigonométriques inverses)
[PDF] 254 Compléments (fonctions trigonométriques inverses)
Comme 0? ? 2 ? y ?? on obtient arcsin(x)+arccos(x)= y + arcos(cos( ? 2 ? y)) = ? 2 III La fonction arctan: la fonction tangente est monotone (
 [PDF] Chapitre12 : Fonctions circulaires réciproques - Melusine
[PDF] Chapitre12 : Fonctions circulaires réciproques - Melusine
D'où comme pour Arcsin Arccos est de classe c8 sur ] ´ 1 1[ ‚ Arccos n'est pas dérivable en ´1 ni en 1 mais sa courbe présente aux points d'abscisses ´1 et
 Etude des fonctions arccos arcsin et arctan - Méthode Maths
Etude des fonctions arccos arcsin et arctan - Méthode Maths
Comme expliqué dans le cours sur les fonctions réciproques la courbe de arcsin est la symétrique de celle de sin par rapport à la droite d'équation y = x mais
 [PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
[PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
%2520d%25C3%25A9riv%25C3%25A9es
 [PDF] [PDF] Exo7 - Exercices de mathématiques
[PDF] [PDF] Exo7 - Exercices de mathématiques
I : Incontournable T : pour travailler et mémoriser le cours Exercice 1 ***IT 1 f1(x) = arcsin ( x ?1+x2 ) 2 f2(x) = arccos ( 1?x2 1+x2 )
 [PDF] I Propriétés fondamentales - Normale Sup
[PDF] I Propriétés fondamentales - Normale Sup
Groupe-cours 51 Sur le cercle trigonométrique (cercle de centre (00) et de rayon 1) on définit la III 2 Les fonctions arccos arcsin arctan
 Arccos Arcsin et Arctan : Cours et exercices corrigés
Arccos Arcsin et Arctan : Cours et exercices corrigés
13 fév 2023 · Arccos Arcsin et Arctan : Les trois fonctions réciproques des fonctions trigonométriques avec le cours détaillé et des exercices corrigés
 [PDF] Cours-3-Complements-trigonometriepdf
[PDF] Cours-3-Complements-trigonometriepdf
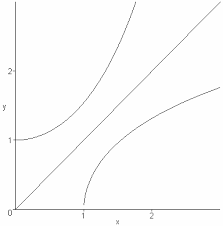
Etude de la fonction Arccos() Arccos:[ 1; 1] [0; ] ? ? + ? fonction ni paire ni impaire non-périodique y=sin(x) y=Arcsin(x)
Fonctions usuelles
de nouvelles fonctions : ch, sh, th, arccos, arcsin, arctan, Argch, Argsh, Argth.Ces fonctions apparaissent naturellement dans la résolution de problèmes simples, en particulier issus de la physique.
Par exemple lorsqu"un fil est suspendu entre deux poteaux (ou un collier tenu entre deux mains) alors la courbe
dessinée est unechaînettedont l"équation fait intervenir le cosinus hyperbolique et un paramètrea(qui dépend de la
longueur du fil et de l"écartement des poteaux) : y=achxa1. Logarithme et exponentielle
1.1. LogarithmeProposition 1.
Il existe une unique fonction, notéeln :]0,+1[!Rtelle que : ln0(x) =1x
(pour tout x>0)etln(1) =0. De plus cette fonction vérifie (pour tout a,b>0) :1.ln(ab) =lna+lnb,
2.ln(1a
) =lna,3.ln(an) =nlna, (pour tout n2N)
4.lnest une fonction continue, strictement croissante et définit une bijection de]0,+1[surR,
5.limx!0ln(1+x)x
=1, 6. la fonction lnest concave etlnx6x1(pour tout x>0). FONCTIONS USUELLES1. LOGARITHME ET EXPONENTIELLE2xy lnxe1 10Remarque.
lnxs"appelle lelogarithme naturelou aussilogarithme néperien. Il est caractérisé parln(e) =1. On définit le
logarithme en baseapar log a(x) =ln(x)ln(a)De sorte que log
a(a) =1.Poura=10on obtient lelogarithme décimallog10qui vérifielog10(10) =1(et donclog10(10n) =n). Dans la
pratique on utilise l"équivalence :x=10y()y=log10(x)En informatique intervient aussi le logarithme en base 2 : log
2(2n) =n.
Démonstration.
L"existence et l"unicité viennent de la théorie de l"intégrale :ln(x) =Rx 11t dt. Passons aux propriétés.1.Posonsf(x) =ln(x y)ln(x)oùy>0est fixé. Alorsf0(x) =yln0(x y)ln0(x) =yx y
1x=0. Doncx7!f(x)a
une dérivée nulle, donc est constante et vautf(1) =ln(y)ln(1) =ln(y). Donc ln(x y)ln(x) =ln(y).
2.D"une part ln (a1a
) =lna+ln1a , mais d"autre part ln(a1a ) =ln(1) =0. Donc lna+ln1a =0. 3.Similaire ou récurrence.
4. ln est dérivable donc continue,ln0(x) =1x >0donc la fonction est strictement croissante. Commeln(2)>ln(1) =0 alorsln(2n) =nln(2)!+1(lorsquen!+1). Donclimx!+1lnx= +1. Delnx=ln1xon déduitlimx!0lnx=1. Par le théorème sur les fonctions continues et strictement croissantes,ln:]0,+1[!Rest
une bijection. 5. lim x!0ln(1+x)x est la dérivée de ln au pointx0=1, donc cette limite existe et vaut ln0(1) =1. 6. ln 0 (x) =1xest décroissante, donc la fonctionlnest concave. Posonsf(x) =x1lnx;f0(x) =11x. Par une étude de fonctionfatteint son minimum enx0=1. Doncf(x)>f(1) =0. Donc lnx6x1.1.2. ExponentielleDéfinition 1.
La bijection réciproque de ln :]0,+1[!Rs"appelle la fonctionexponentielle, notée exp :R!]0,+1[.
FONCTIONS USUELLES1. LOGARITHME ET EXPONENTIELLE3xyexpxe 1 10Pourx2Ron note aussiexpour expx.Proposition 2.
La fonction exponentielle vérifie les propriétés suivantes : •exp(lnx) =x pour tout x>0etln(expx) =x pour tout x2R• exp(a+b) =exp(a)exp(b) exp(nx) = (expx)n exp:R!]0,+1[est une fonction continue, strictement croissante vérifiantlimx!1expx=0et limx!+1exp= +1.La fonction exponentielle est dérivable etexp0x=expx, pour tout x2R. Elle est convexe etexpx>1+x.Remarque.
La fonction exponentielle est l"unique fonction qui vérifieexp0(x) =exp(x)(pour toutx2R) etexp(1) =e. Où
e'2,718... est le nombre qui vérifie lne=1.Démonstration.Ce sont les propriétés du logarithme retranscrites pour sa bijection réciproque.
Par exemple pour la dérivée : on part de l"égalitéln(expx) =xque l"on dérive. Cela donneexp0(x)ln0(expx) =1
donc exp0(x)1expx=1 et ainsi exp0(x) =expx.1.3. Puissance et comparaisonPar définition, poura>0 etb2R,a
b=expblnaRemarque. •pa=a12 =exp12 lna npa=a1n =exp1n lna(laracinen-èmedea) On note aussi expxparexce qui se justifie par le calcul :ex=expxlne=exp(x).Les fonctionsx7!axs"appellent aussi des fonctions exponentielles et se ramènent systématiquement à la fonction
exponentielle classique par l"égalitéax=exp(xlna). Il ne faut surtout pas les confondre avec les fonctions
puissancesx7!xa.Proposition 3.Soit x,y>0et a,b2R.
•x a+b=xaxb•x a=1x a•(x y)a=xaya•(xa)b=xabFONCTIONS USUELLES1. LOGARITHME ET EXPONENTIELLE4•ln(xa) =alnxComparons les fonctions lnx, expxavecx:Proposition 4.
lim x!+1lnxx =0etlimx!+1expxx = +1.xyx a(a>1)x a(a<1)expxlnxx 1 10Démonstration.
1. On a vu ln x6x1 (pour toutx>0). Donc lnx6xdonclnpxpx61. Cela donne
06lnxx
=lnpx2x
=2lnpx x =2lnpxpx 1px 62pxCette double inégalité entraîne lim
x!+1lnxx =0. 2. On a vu exp x>1+x(pour toutx2R). Donc expx!+1(lorsquex!+1). xexpx=ln(expx)expx=lnuuLorsquex!+1alorsu=expx!+1et donc par le premier pointlnuu !0. Doncxexpx!0et reste positive, ainsi limx!+1expxx = +1.Mini-exercices. 1.Montrer que ln (1+ex) =x+ln(1+ex), pour toutx2R.
2.Étudier la fonctionf(x) =ln(x2+1)ln(x)1. Tracer son graphe. Résoudre l"équation(f(x) =0). Idem avec
g(x) =1+lnxx . Idem avech(x) =xx. 3.Expliquer comment log
10permet de calculer le nombre de chiffres d"un entiern.
4. Montrerln(1+x)>xx22pourx>0(faire une étude de fonction). Idem avecex>1+x+x22pour toutx>0. 5. Calculer la limite de la suite définie par un=1+1n nlorsquen!+1. Idem avecvn=1n netwn=n1n FONCTIONS USUELLES2. FONCTIONS CIRCULAIRES INVERSES52. Fonctions circulaires inverses
2.1. ArccosinusConsidérons la fonction cosinuscos:R![1,1],x7!cosx. Pour obtenir une bijection à partir de cette fonction,
il faut considérer la restriction de cosinus à l"intervalle[0,]. Sur cet intervalle la fonction cosinus est continue et
strictement décroissante, donc la restriction cos j:[0,]![1,1] est une bijection. Sa bijection réciproque est la fonctionarccosinus: arccos :[1,1]![0,]xy cosx0 22+11xy
arccosx011 2 On a donc, par définition de la bijection réciproque : cos arccos(x)=x8x2[1,1] arccoscos(x)=x8x2[0,]Autrement dit : Six2[0,]cos(x) =y()x=arccosyTerminons avec la dérivée de arccos : arccos0(x) =1p1x28x2]1,1[Démonstration.On démarre de l"égalité cos(arccosx) =xque l"on dérive :
cos(arccosx) =x =) arccos0(x)sin(arccosx) =1 =)arccos0(x) =1sin(arccosx) =)arccos0(x) =1p1cos2(arccosx)() =)arccos0(x) =1p1x2FONCTIONS USUELLES2. FONCTIONS CIRCULAIRES INVERSES6Le point crucial()se justifie ainsi : on démarre de l"égalitécos2y+sin2y=1, en substituanty=arccosxon obtient
cos2(arccosx)+sin2(arccosx) =1doncx2+sin2(arccosx) =1. On en déduit :sin(arccosx) = +p1x2(avec le signe+car arccosx2[0,], et donc on a sin(arccosx)>0).2.2. ArcsinusLa restriction
sin j:[2 ,+2 ]![1,1] est une bijection. Sa bijection réciproque est la fonctionarcsinus: arcsin :[1,1]![2 ,+2 ]xysinx0 22+11xy
arcsinx011 2 2 sin arcsin(x)=x8x2[1,1] arcsinsin(x)=x8x2[2 ,+2 ]Six2[2 ,+2 ]sin(x) =y()x=arcsinyarcsin0(x) =1p1x28x2]1,1[2.3. Arctangente
La restriction
tan j:]2 ,+2 [!R est une bijection. Sa bijection réciproque est la fonctionarctangente: arctan :R!]2 ,+2 FONCTIONS USUELLES3. FONCTIONS HYPERBOLIQUES ET HYPERBOLIQUES INVERSES7xytanx 2 232xyarctanx0 2 2 tan arctan(x)=x8x2R arctantan(x)=x8x2]2 ,+2 [Six2]2 ,+2 [tan(x) =y()x=arctanyarctan
0(x) =11+x28x2RMini-exercices.
1.Calculer les valeurs de arccos et arcsin en 0, 1,
12 ,p2 2 ,p3 2 . Idem pour arctan en 0, 1,p3 et 1p3 2.Calculer arccos (cos73
). Idem avec arcsin(sin73 )et arctan(tan73 )(attention aux intervalles!) 3. Calculer cos (arctanx), cos(arcsinx), tan(arcsinx). 4. Calculer la dérivée de f(x) =arctanxp1x2 . En déduire quef(x) =arcsinx, pour toutx2]1,1[. 5.Montrer que arccos x+arcsinx=2
, pour toutx2[1,1].3. Fonctions hyperboliques et hyperboliques inverses3.1. Cosinus hyperbolique et son inverse
Pourx2R, lecosinus hyperboliqueest :chx=ex+ex2
La restriction ch
j:[0,+1[![1,+1[est une bijection. Sa bijection réciproque est Argch :[1,+1[![0,+1[. FONCTIONS USUELLES3. FONCTIONS HYPERBOLIQUES ET HYPERBOLIQUES INVERSES8xychxshx1 10 xyArgchxArgshx1
103.2. Sinus hyperbolique et son inverse
Pourx2R, lesinus hyperboliqueest :shx=exex2
sh:R!Rest une fonction continue, dérivable, strictement croissante vérifiantlimx!1shx=1et limx!+1shx= +1, c"est donc une bijection. Sa bijection réciproque est Argsh :R!R.Proposition 5. ch2xsh2x=1 ch0x=shx,sh0x=chxArgsh :R!Rest strictement croissante et continue.
Argshest dérivable etArgsh0x=1px
2+1.Argshx=lnx+px
2+1Démonstration.
ch2xsh2x=14 (ex+ex)2(exex)2=14 (e2x+2+e2x)(e2x2+e2x)=1. ddx (chx) =ddx e x+ex2 =exex2 =shx. Idem pour la dérivée de shx.Car c"est la réciproque de sh.
Comme la fonctionx7!sh0xne s"annule pas surRalors la fonctionArgshest dérivable surR. On calcule la
dérivée par dérivation de l"égalité sh(Argshx) =x: Argsh0x=1ch(Argshx)=1AE
sh2(Argshx)+1=1px
2+1Notonsf(x) =lnx+px
2+1alors
f0(x) =1+xpx
2+1x+px
2+1=1px
2+1=Argsh0x
Comme de plusf(0) =ln(1) =0etArgsh0=0(carsh0=0), on en déduit que pour toutx2R,f(x) =Argshx. FONCTIONS USUELLES3. FONCTIONS HYPERBOLIQUES ET HYPERBOLIQUES INVERSES93.3. Tangente hyperbolique et son inverse
Par définition latangente hyperboliqueest :thx=shxchxLa fonction th :R!]1,1[est une bijection, on note Argth :]1,1[!Rsa bijection réciproque.xy
thx110xyArgthx110
3.4. Trigonométrie hyperbolique
ch2xsh2x=1
ch(a+b) =chachb+shashb ch(2a) =ch2a+sh2a=2 ch2a1=1+2 sh2a sh(a+b) =shachb+shbcha sh(2a) =2 shacha th(a+b) =tha+thb1+thathb chquotesdbs_dbs7.pdfusesText_13[PDF] appréciation 3eme trimestre primaire
[PDF] y=ax+b signification
[PDF] je cherche quelqu'un pour m'aider financièrement
[PDF] recherche aide a domicile personnes agées
[PDF] aide personne agée offre d'emploi
[PDF] tarif garde personne agée ? domicile
[PDF] y=ax+b graphique
[PDF] ménage chez personnes agées
[PDF] garde personne agee a son domicile
[PDF] cherche a garder personne agee a domicile
[PDF] calcul arithmétique de base
[PDF] ax2 bx c determiner a b et c
[PDF] opération arithmétique binaire
[PDF] rôle de la vitamine d dans l'organisme
