 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Or arccos(x) ∈]0π[ et sin(arccos(x)) > 0. Donc sin(arccos(x)) = √1 - x2 1 Représentez la fonction x ↦→ arcsin(sin(x)). 2 Représentez la fonction x ...
 Chapitre12 : Fonctions circulaires réciproques
Chapitre12 : Fonctions circulaires réciproques
D'où comme pour Arcsin
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
f3(x) = arcsin√1−x2 −arctan. (√. 1−x. 1+x. ) . 4. f4(x) = arctan 1. 2x2 −π +2kπ ⩽ x < 2kπ alors arccos(cosx) = arccos(cos(2kπ −x)) = 2kπ −x avec k ...
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
tan(x) = y ⇐⇒ x = arctan y arctan (x) = 1. 1 + x2. ∀x ∈. Mini-exercices. 1. Calculer les valeurs de arccos et arcsin en 0 1
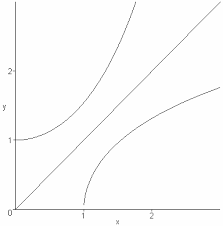 Cours3 Compléments trigonométrie
Cours3 Compléments trigonométrie
sin(Arcsin( )) cos(Arcsin( )) Si deux nombres sont égaux alors ils ont la même tangente (mais la réciproque est fausse) donc… SI Arctan( ) Arctan(4) Arctan(5).
 1) La fonction Arccos.
1) La fonction Arccos.
Par le cours on en déduit que sa fonction réciproque Arccos est dérivable exemple Arctan(tan(3π)) = Arctan(0) = 0. Question : si x est un réel tel que x ...
 I Propriétés fondamentales
I Propriétés fondamentales
Groupe-cours 51. MAT1112 - Calcul Le graphe de f−1 est le symétrique du graphe de f par rapport à la droite y = x. III.2 Les fonctions arccos arcsin
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
arccosarcsin
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Chapitre12 : Fonctions circulaires réciproques
Chapitre12 : Fonctions circulaires réciproques
4.0 International ». https://www.immae.eu/cours/. Chapitre12 : Fonctions circulaires D'où comme pour Arcsin
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Cours magistral 4 : Réciproques des fonctions trigonométriques sin(arccos(x))? Ce que l'on sait cos(arccos(x)) = x et ... arcsin(sin(x)) = x Vx ? [-?.
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
ter à notre catalogue de nouvelles fonctions : chsh
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
de nouvelles fonctions : ch sh
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 2.5.4 Compléments (fonctions trigonométriques inverses)
2.5.4 Compléments (fonctions trigonométriques inverses)
arcsin(x)+arccos(x)= y + arcos(cos( ?. 2. ? y)) = ?. 2 . III. La fonction arctan: la fonction tangente est monotone (strictement croissante) sur
 TD 1 Intégrales généralisées
TD 1 Intégrales généralisées
16 sept. 2016 Résumé de cours. 2. Exercices. ... Arctan etc) n'ont pas toujours de primitives élémentaires. ... Arcsin d – Arcsin c
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
I : Incontournable T : pour travailler et mémoriser le cours 3. f3(x) = arcsin?1?x2 ?arctan ... 2sinxcosx(arcsin(
 Résumé des propriétés des fonctions trigonométriques
Résumé des propriétés des fonctions trigonométriques
réciproques arcsin arccos et arctan. Résumé de cours sur les nombres complexes. Le nombre imaginaire i est introduit comme solution de x2 = ?1 et vérifie
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
cours du mercredi 1/3/17 Chapitre V Fonctions arcsin arccos arctan 1 Définitions 1 1 arcsin Proposition 1 1 La fonction sin : [??/2 ?/2] ? [?11]
 [PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
[PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
décroissante donc est une bijection Sa bijection réciproque est la fonction arccosinus : { cos(x) = y x ? [0?] ? { x = arccos(y) y ? [-11]
 [PDF] 254 Compléments (fonctions trigonométriques inverses)
[PDF] 254 Compléments (fonctions trigonométriques inverses)
Comme 0? ? 2 ? y ?? on obtient arcsin(x)+arccos(x)= y + arcos(cos( ? 2 ? y)) = ? 2 III La fonction arctan: la fonction tangente est monotone (
 [PDF] Chapitre12 : Fonctions circulaires réciproques - Melusine
[PDF] Chapitre12 : Fonctions circulaires réciproques - Melusine
D'où comme pour Arcsin Arccos est de classe c8 sur ] ´ 1 1[ ‚ Arccos n'est pas dérivable en ´1 ni en 1 mais sa courbe présente aux points d'abscisses ´1 et
 Etude des fonctions arccos arcsin et arctan - Méthode Maths
Etude des fonctions arccos arcsin et arctan - Méthode Maths
Comme expliqué dans le cours sur les fonctions réciproques la courbe de arcsin est la symétrique de celle de sin par rapport à la droite d'équation y = x mais
 [PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
[PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
%2520d%25C3%25A9riv%25C3%25A9es
 [PDF] [PDF] Exo7 - Exercices de mathématiques
[PDF] [PDF] Exo7 - Exercices de mathématiques
I : Incontournable T : pour travailler et mémoriser le cours Exercice 1 ***IT 1 f1(x) = arcsin ( x ?1+x2 ) 2 f2(x) = arccos ( 1?x2 1+x2 )
 [PDF] I Propriétés fondamentales - Normale Sup
[PDF] I Propriétés fondamentales - Normale Sup
Groupe-cours 51 Sur le cercle trigonométrique (cercle de centre (00) et de rayon 1) on définit la III 2 Les fonctions arccos arcsin arctan
 Arccos Arcsin et Arctan : Cours et exercices corrigés
Arccos Arcsin et Arctan : Cours et exercices corrigés
13 fév 2023 · Arccos Arcsin et Arctan : Les trois fonctions réciproques des fonctions trigonométriques avec le cours détaillé et des exercices corrigés
 [PDF] Cours-3-Complements-trigonometriepdf
[PDF] Cours-3-Complements-trigonometriepdf
Etude de la fonction Arccos() Arccos:[ 1; 1] [0; ] ? ? + ? fonction ni paire ni impaire non-périodique y=sin(x) y=Arcsin(x)
Trigonométrie hyperbolique
* très facile ** facile *** difficulté moyenne **** difficile ***** très difficile I : Incontournable T : pour travailler et mémoriser le cours Exercice 1***ITDomaine de définition et calcul des fonctions suivantes :1.x7!sin(arcsinx),
2.x7!arcsin(sinx),
3.x7!cos(arccosx),
4.x7!arccos(cosx),
5.x7!tan(arctanx),
6.x7!arctan(tanx).
2.Calculer arctan x+arctan1x
pourxréel non nul. 3. Calculer cos (arctana)et sin(arctana)pouraréel donné. 4. Calculer ,pour aetbréels tels queab6=1, arctana+arctanben fonction de arctana+b1ab(on étudiera d"abord cos(arctana+arctanb)et on distinguera les casab<1,ab>1 eta>0,ab>1 eta<0).Rsin2x
0arcsinpt dt+Rcos2x
0arccospt dt.
1.f1(x) =arcsinxp1+x2
2.f2(x) =arccos1x21+x2
13.f3(x) =arcsinp1x2arctan
q1x1+x4.f4(x) =arctan12x2arctanxx+1+arctanx1x
12 +arctan15 +arctan182+arctan22
2+:::+arctan2n
(Utiliser l"exercice 2 4)) f(x) = (x21)arctan12x1; et on appelle(C)sa courbe représentative dans un repère orthonormé. 1.Quel est l"ensemble de définition Ddef?
2. Exprimer ,sur Dnf0g, la dérivée defsous la forme :f0(x) =2xg(x). 3. Montrer que : 8x2R;2x44x3+9x24x+1>0 et en déduire le tableau de variation deg. 4.Dresser le tableau de v ariationde f.
2. En déduire la v aleurde un=20th(20x)+21th(21x)++2nth(2nx)pournentier naturel non nul etx réel non nul donnés puis calculer la limite de(un). 1. sin (2arcsinx), 22.cos (2arccosx),
3. sin2arccosx2
4. ln (px2+1+x)+ln(px
2+1x),
5. ar gsh x212x 6. ar gch(2x21), 7. ar gth qchx1chx+1 8. ch(lnx)+sh(lnx)x 1. ch x=2, 2. arcsin (2x) =arcsinx+arcsin(xp2), 3.2 arcsinx=arcsin(2xp1x2).
Correction del"exer cice1 Narcsinxexiste si et seulement sixest dans[1;1]. Donc, sin(arcsinx)existe si et seulement sixest dans[1;1]
et pourxdans[1;1], sin(arcsinx) =x. arcsin(sinx)existe pour tout réelxmais ne vautxque sixest dansp2 ;p2 . • S"il existe un entier relatifktel quep2 +2kp6xDe plus, on ak6x2p+14
0(x) =1p1x21p1x2=0:
Doncfest constante sur[1;1]et pourxdans[1;1],f(x) =f(0) =p28x2[1;1];arccosx+arcsinx=p2
:2ème solution. Il existe un unique réelqdans[0;p]tel quex=cosq, à savoirq=arccosx. Mais alors,
arccosx+arcsinx=q+arcsin sin(p2 q) =q+p2 q=p2 (car p2 qest dans[p2 ;p22.1ère solution. Pourxréel non nul, posonsf(x) =arctanx+arctan1x
.fest impaire.fest dérivable surRet pour tout réelxnon nul,f0(x) =11+x21x211+1x
2=0.fest donc constante sur]¥;0[et sur
]0;+¥[(mais pas nécessairement surR). Donc, pourx>0,f(x) =f(1) =2arctan1=p2 , et puisquef est impaire, pourx<0,f(x) =f(x) =p2 . Donc,8x2R;arctanx+arctan1x
p2 six>0 p2 six<0=p2 sgn(x):42èmesolutionPourxréelstrictementpositifdonné, ilexisteununiqueréelqdans0;p2
telquex=tanqà savoirq=arctanx. Mais alors,
arctanx+arctan1x =q+arctan1tanq =q+arctan tan(p2 q) =q+p2 q=p2 (carqetp2 qsont éléments de0;p2 3. cos2(arctana) =11+tan2(arctana)=11+a2. De plus , arctanaest dans]p2
;p2 [et donc cos(arctana)>0. On en déduit que pour tout réela, cos(arctana) =1p1+a2puis sin(arctana) =cos(arctana)tan(arctana) =ap1+a2:8a2R;cos(arctana) =11+a2et sin(arctana) =ap1+a2:4.D"après 3),
cos(arctana+arctanb) =cos(arctana)cos(arctanb)sin(arctana)sin(arctanb) =1abp1+a2p1+b2;ce qui montre déjà , puisqueab6=1, que cos(arctana+arctanb)6=0 et donc que tan(arctana+arctanb)
existe. On a immédiatement, tan(arctana+arctanb) =a+b1ab:Maintenant, arctana+arctanbest dansp;p2
[p2 ;p2 [p2 ;p.1er cas.Siab<1 alors cos(arctana+arctanb)>0 et donc arctana+arctanbest dansp2
;p2 . Dans ce cas, arctana+arctanb=arctana+b1ab.2ème cas.Siab>1 alors cos(arctana+arctanb)<0 et donc arctana+arctanbest dansp;p2
[p2 ;p.Si de plusa>0, arctana+arctanb>p2
et donc arctana+arctanbest dansp2 ;p. Dans ce cas, arctana+arctanbpest dansp2 ;p2 et a même tangente que arctana+b1ab. Donc, arctana+ arctanb=arctana+b1ab+p. Sia<0, on trouve de même arctana+arctanb=arctana+b1abp.En résumé,
arctana+arctanb=8 >:arctan a+b1absiab<1 arctan a+b1ab+psiab>1 eta>0 arctan a+b1abpsiab>1 eta<0:Correction del"exer cice3 Nch(a+b) =chachb+shashbet ch(ab) =chachbshashb; sh(a+b) =shachb+chashbet sh(ab) =shachbshbcha th(a+b) =tha+thb1+thathbet th(ab) =thathb1thathb:5Deux démonstrations :
chachb+shashb=14 ((ea+ea)(eb+eb)+(eaea)(ebeb)) =12 (ea+b+eab) =ch(a+b): th(a+b) =sh(a+b)ch(a+b)=shachb+shbchachachb+shashb=tha+thb1+thathbaprès division du numérateur et du dénominateur par le nombre non nul chachb. En appliquant àa=b=x,
on obtient :8x2R;ch(2x) =ch2x+sh2x=2ch2x1=2sh2x+1;sh(2x) =2shxchxet th(2x) =2thx1+th2x:En additionnant entre elles les formules d"addition, on obtient les formules de linéarisation :
chachb=12 (ch(a+b)+ch(ab));shashb=12 (ch(a+b)ch(ab))et shachb=12 (sh(a+b)+sh(ab)); et en particulier ch2x=ch(2x)+12
et sh2x=ch(2x)12 :Correction del"exer cice4 NPourxréel, on posef(x) =Rsin2x0arcsinpt dt+Rcos2x
0arccospt dt.
La fonctiont7!arcsinptest continue sur[0;1]. Donc, la fonctiony7!Ry0arcsinpt dtest définie et dérivable
sur[0;1]. De plus,x7!sin2xest définie et dérivable surRà valeurs dans[0;1]. Finalement, la fonction
x7!Rsin2x0arcsinpt dtest définie et dérivable surR. De même, la fonctiont7!arccosptest continue sur[0;1].
Donc, la fonctiony7!Ry
0arccospt dtest définie et dérivable sur[0;1]. De plus, la fonctionx7!cos2xest
définie et dérivable surR, à valeurs dans[0;1]. Finalement, la fonctionx7!Rcos2x0arccospt dtest définie et
dérivable surR. Donc,fest définie et dérivable surRet, pour tout réelx, f0(x) =2sinxcosxarcsin(psin
2x)2sinxcosxarccos(pcos
2x) On note alors quefestp-pérodique et paire. Pourxélément de[0;p2 ],f0(x) =2sinxcosx(xx) =0.fest donc constante sur[0;p2 ]et pourxélément de[0;p2 ],f(x) =fp4 =R1=20arcsinpt dt+R1=2
0arccosptdt=R1=2
0p2 dt=p4 . Mais alors, par parité etp-périodicité,8x2R;Rsin2x
0arcsinpt dt+Rcos2x
0arccospt dt=p4
:Correction del"exer cice5 N1.1ère solution.Pour tout réelx,px2+1>px
2=jxjet donc1 2+1<1. Ainsif1est définie et
dérivable surR, impaire, et pour tout réelx, f 01(x) =1px
2+112 x2x(x2+1)px 2+1 1q 1x21+x2=11+x2=arctan0(x):
Donc il existe une constante réelleCtelle que pour tout réelx,f1(x) =arctanx+C.x=0 fournitC=0 et donc, 6 8x2R;arcsinxpx
2+1 =arctanx:2ème solution.Pourxréel donné, posonsq=arctanx.qest dansp2 ;p2 etx=tanq. xpxquotesdbs_dbs7.pdfusesText_13
2+1<1. Ainsif1est définie et
dérivable surR, impaire, et pour tout réelx, f01(x) =1px
2+112 x2x(x2+1)px 2+1 1q1x21+x2=11+x2=arctan0(x):
Donc il existe une constante réelleCtelle que pour tout réelx,f1(x) =arctanx+C.x=0 fournitC=0 et donc, 68x2R;arcsinxpx
2+1 =arctanx:2ème solution.Pourxréel donné, posonsq=arctanx.qest dansp2 ;p2 etx=tanq. xpxquotesdbs_dbs7.pdfusesText_13[PDF] appréciation 3eme trimestre primaire
[PDF] y=ax+b signification
[PDF] je cherche quelqu'un pour m'aider financièrement
[PDF] recherche aide a domicile personnes agées
[PDF] aide personne agée offre d'emploi
[PDF] tarif garde personne agée ? domicile
[PDF] y=ax+b graphique
[PDF] ménage chez personnes agées
[PDF] garde personne agee a son domicile
[PDF] cherche a garder personne agee a domicile
[PDF] calcul arithmétique de base
[PDF] ax2 bx c determiner a b et c
[PDF] opération arithmétique binaire
[PDF] rôle de la vitamine d dans l'organisme
