 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Or arccos(x) ∈]0π[ et sin(arccos(x)) > 0. Donc sin(arccos(x)) = √1 - x2 1 Représentez la fonction x ↦→ arcsin(sin(x)). 2 Représentez la fonction x ...
 Chapitre12 : Fonctions circulaires réciproques
Chapitre12 : Fonctions circulaires réciproques
D'où comme pour Arcsin
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
f3(x) = arcsin√1−x2 −arctan. (√. 1−x. 1+x. ) . 4. f4(x) = arctan 1. 2x2 −π +2kπ ⩽ x < 2kπ alors arccos(cosx) = arccos(cos(2kπ −x)) = 2kπ −x avec k ...
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
tan(x) = y ⇐⇒ x = arctan y arctan (x) = 1. 1 + x2. ∀x ∈. Mini-exercices. 1. Calculer les valeurs de arccos et arcsin en 0 1
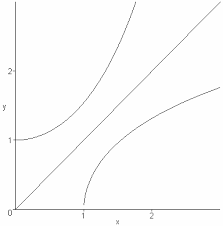 Cours3 Compléments trigonométrie
Cours3 Compléments trigonométrie
sin(Arcsin( )) cos(Arcsin( )) Si deux nombres sont égaux alors ils ont la même tangente (mais la réciproque est fausse) donc… SI Arctan( ) Arctan(4) Arctan(5).
 1) La fonction Arccos.
1) La fonction Arccos.
Par le cours on en déduit que sa fonction réciproque Arccos est dérivable exemple Arctan(tan(3π)) = Arctan(0) = 0. Question : si x est un réel tel que x ...
 I Propriétés fondamentales
I Propriétés fondamentales
Groupe-cours 51. MAT1112 - Calcul Le graphe de f−1 est le symétrique du graphe de f par rapport à la droite y = x. III.2 Les fonctions arccos arcsin
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
arccosarcsin
 Chapitre V Fonctions arcsin arccos
Chapitre V Fonctions arcsin arccos
http://math.univ-lyon1.fr/~tchoudjem/ENSEIGNEMENT/L1/cours10.pdf
 Chapitre12 : Fonctions circulaires réciproques
Chapitre12 : Fonctions circulaires réciproques
4.0 International ». https://www.immae.eu/cours/. Chapitre12 : Fonctions circulaires D'où comme pour Arcsin
 Cours de Mathématiques L1 Semestre 1
Cours de Mathématiques L1 Semestre 1
Cours magistral 4 : Réciproques des fonctions trigonométriques sin(arccos(x))? Ce que l'on sait cos(arccos(x)) = x et ... arcsin(sin(x)) = x Vx ? [-?.
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
ter à notre catalogue de nouvelles fonctions : chsh
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
de nouvelles fonctions : ch sh
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 2.5.4 Compléments (fonctions trigonométriques inverses)
2.5.4 Compléments (fonctions trigonométriques inverses)
arcsin(x)+arccos(x)= y + arcos(cos( ?. 2. ? y)) = ?. 2 . III. La fonction arctan: la fonction tangente est monotone (strictement croissante) sur
 TD 1 Intégrales généralisées
TD 1 Intégrales généralisées
16 sept. 2016 Résumé de cours. 2. Exercices. ... Arctan etc) n'ont pas toujours de primitives élémentaires. ... Arcsin d – Arcsin c
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
I : Incontournable T : pour travailler et mémoriser le cours 3. f3(x) = arcsin?1?x2 ?arctan ... 2sinxcosx(arcsin(
 Résumé des propriétés des fonctions trigonométriques
Résumé des propriétés des fonctions trigonométriques
réciproques arcsin arccos et arctan. Résumé de cours sur les nombres complexes. Le nombre imaginaire i est introduit comme solution de x2 = ?1 et vérifie
 [PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
[PDF] Chapitre V Fonctions arcsin arccos arctan 1 Définitions 2 Propriétés
cours du mercredi 1/3/17 Chapitre V Fonctions arcsin arccos arctan 1 Définitions 1 1 arcsin Proposition 1 1 La fonction sin : [??/2 ?/2] ? [?11]
 [PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
[PDF] Cours magistral 4 : Réciproques des fonctions trigonométriques
décroissante donc est une bijection Sa bijection réciproque est la fonction arccosinus : { cos(x) = y x ? [0?] ? { x = arccos(y) y ? [-11]
 [PDF] 254 Compléments (fonctions trigonométriques inverses)
[PDF] 254 Compléments (fonctions trigonométriques inverses)
Comme 0? ? 2 ? y ?? on obtient arcsin(x)+arccos(x)= y + arcos(cos( ? 2 ? y)) = ? 2 III La fonction arctan: la fonction tangente est monotone (
 [PDF] Chapitre12 : Fonctions circulaires réciproques - Melusine
[PDF] Chapitre12 : Fonctions circulaires réciproques - Melusine
D'où comme pour Arcsin Arccos est de classe c8 sur ] ´ 1 1[ ‚ Arccos n'est pas dérivable en ´1 ni en 1 mais sa courbe présente aux points d'abscisses ´1 et
 Etude des fonctions arccos arcsin et arctan - Méthode Maths
Etude des fonctions arccos arcsin et arctan - Méthode Maths
Comme expliqué dans le cours sur les fonctions réciproques la courbe de arcsin est la symétrique de celle de sin par rapport à la droite d'équation y = x mais
 [PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
[PDF] Tableaux (formulaires fonctions usuelles dérivées primitives - 2013
%2520d%25C3%25A9riv%25C3%25A9es
 [PDF] [PDF] Exo7 - Exercices de mathématiques
[PDF] [PDF] Exo7 - Exercices de mathématiques
I : Incontournable T : pour travailler et mémoriser le cours Exercice 1 ***IT 1 f1(x) = arcsin ( x ?1+x2 ) 2 f2(x) = arccos ( 1?x2 1+x2 )
 [PDF] I Propriétés fondamentales - Normale Sup
[PDF] I Propriétés fondamentales - Normale Sup
Groupe-cours 51 Sur le cercle trigonométrique (cercle de centre (00) et de rayon 1) on définit la III 2 Les fonctions arccos arcsin arctan
 Arccos Arcsin et Arctan : Cours et exercices corrigés
Arccos Arcsin et Arctan : Cours et exercices corrigés
13 fév 2023 · Arccos Arcsin et Arctan : Les trois fonctions réciproques des fonctions trigonométriques avec le cours détaillé et des exercices corrigés
 [PDF] Cours-3-Complements-trigonometriepdf
[PDF] Cours-3-Complements-trigonometriepdf
Etude de la fonction Arccos() Arccos:[ 1; 1] [0; ] ? ? + ? fonction ni paire ni impaire non-périodique y=sin(x) y=Arcsin(x)
Intégrales généralisées
1. Résumé de cours.
2. Exercices.
Pierre-Jean Hormière
____________ " Si vous avez tout compris, c"est que je n"ai pas été clair. »Albert Einstein
1. Résumé de cours.
1.1. Intégration sur un segment
On nomme segment un intervalle fermé borné de la droite réelle R. Soient I = [a, b] un segment de R, f une fonction I ® R. Si f est à valeurs positives, on appelle intégrale de f sur le segment I l"aire du domaineD = { (x, y) Î I´R ; 0 £ y £ f(x) }.
On note alors
b adxxf).( = Aire(D). Si f est à valeurs réelles, on appelle intégrale de f sur le segment I la différence de l"aire du domaine D + = { (x, y) Î I´R ; 0 £ f(x) et 0 £ y £ f(x) } et de l"aire du domaine D - = { (x, y) Î I´R ; f(x) £ 0 et f(x) £ y £ 0 }On note alors
b adxxf).( = Aire(D+) - Aire(D-).Il s"agit de l"aire algébrique située entre l"axe Ox et le graphe de f. L"aire arithmétique est alors
donnée par b adxxf.)( = Aire(D+) + Aire(D-). Oui, mais comment définir et calculer cette aire, ces aires ? Cette aire, ces aires, sont-elles toujours définies ? En somme, quelles fonctions sont susceptibles d"intégration ?Pendant vingt siècles, d"Eudoxe et Archimède à Pascal, les mathématiciens considéraient une
subdivision de I, s = (a = x0 < x1 < ... < xn = b), calculaient la somme des aires des tuyaux d"orgue
S = 1 0 1)()( n k kkkfxxx, où pour chaque indice k, xk est un point quelconque du segment [xk, xk+1], puis faisaient tendre le pas de la subdivision s, c"est-à-dire |s| = max (x k+1 - xk), vers 0. On démontre que si f est continue, ou continue par morceaux, alors les sommes S ont une limite,et c"est cette limite que l"on nomme intégrale de f sur I. Pour des fonctions plus générales les
sommes S n"ont pas toujours de limite, et donc l"intégrale n"existe pas toujours.Ainsi, pour calculer l"aire
b adxx². du domaine D = { (x, y) Î I´R ; 0 £ y £ x2 }, Archimède calcule la somme S = 1 0 1)()( n k kkkfxxx = nab-²))(( 10∑
n kabnka , puis fait tendre n vers 0. Il trouve 333ab-.
Essayez !...
Jusqu"en 1664, les mathématiciens n"avaient pas d"autre moyen de calculer des intégrales. La
méthode était longue, fastidieuse, et ne fonctionnait que sur un nombre limité de fonctions. En 1665,
Newton et Leibniz ont découvert indépendamment une méthode révolutionnaire pour calculer
2 l"intégrale d"une fonction continue. Pour calculer∫ b adxxf).(, il suffit de disposer d"une primitive de f, c"est-à-dire d"une fonction F dont la dérivée est f. Et alors b adxxf).( = F(b) - F(a).Ce théorème de Newton-Leibniz est aussi appelé théorème fondamental du calcul différentiel et
intégral, car il établit un pont entre calcul différentiel et calcul intégral. Le calcul d"une intégrale se
ramène au calcul d"une primitive, c"est-à-dire d"une " antidérivée ». Ce théorème a fait faire à
l"analyse un bon spectaculaire au 18 ème siècle. Cependant il s"est heurté à deux sortes de difficultés :· Si toute fonction continue f a bien une primitive F, c"est-à-dire est une dérivée de F, les fonctions
continues élémentaires, c"est-à-dire sommes, produits, quotients, composées de fonctions usuelles
(fonctions rationnelles, logarithmes, exponentielles, puissances, sinus, cosinus, Arcsin, Arccos,
Arctan, etc) n"ont pas toujours de primitives élémentaires. On peut alors enrichir le bestiaire des
fonctions connues en lui adjoignant de nouvelles fonctions, exponentielles-intégrales, elliptiques,
etc., mais cela demande du travail et de l"érudition.· On a besoin d"intégrer des fonctions plus générales que les fonctions continues ou continues par
morceaux à valeurs réelles : fonctions à valeurs complexes ou vectorielles, fonctions discontinues.
Riemann, Darboux, Lebesgue, Kurzweil, Henstock, etc., se sont attelés à ces généralisations.
1.2. Calculs d"intégrales et de primitives
Les deux méthodes principales pour calculer intégrales et primitives sont le changement de variables
et l"intégration par parties.Proposition 1 : Soit F une fonction de classe C
1 de I = [a, b] dans R. Pour toute fonction f continue
de J = F(I) dans E, on a : F F)( b adxxf = ∫FF b adtttf)."()).((.Preuve
: Les fonctions y ®∫ F F)( y adxxf et y ®∫FF y adtttf)."()).(( sont définies et de classe C1 sur[a, b], la première en tant que composée. Elles ont même dérivée f(F(y)).F"(y) et même valeur en a.
Remarque
: En pratique, ce théorème s"utilise dans les deux sens :¾ dans le sens
∫FF b adtttf)."()).(( =∫ F F)( b adxxf , il suffit de poser x = F(t) et le changement de variable " se fait tout seul » dans la forme différentielle w = f(F(t)).F"(t).dt = f(x).dx.Exemples :
∫FF b adttt).(").( = 2 )²()²(abF-F, ∫F Fb adttt.)()(" = ln |)(bF| - ln |)(aF| , ∫+F Fb adttt.1)²()(" = Arctan )(bF - Arctan)(aF, etc.¾ dans le sens
b adxxf).( = ∫FF b adtttf)."()).((, où a = F-1(a) et b = F-1(b), il faut s"assurer queF est C
1 et strictement monotone.
Exemples : calculer
∫-dxx.²1 , ∫+dxx.²1 et ∫-dxx.1². Proposition 2 : Soient u et v deux fonctions [a, b] ® C de classe C1 ; on a :
b adxxvxu)."().( = []b axvxu)().( - ∫ b adxxvxu).()."(. Preuve : u.v est une fonction de classe C1 sur [a, b], et (u.v)" = u".v + u.v".Applications : intégrer les exponentielles-polynômes, calculs récurrents d"intégrales, intégrer
certaines fonctions transcendantes, etc. 31.3. Intégrales généralisées.
Si I est un intervalle quelconque, mais non un segment, y a-t-il moyen de définir ∫Idxxf).( ?Ainsi, en quel sens peut-on affirmer que
1 0 xdx = 2 , que∫¥--dxex.2/² = p2, etc. ?
Définitions : 1) Soient I = [a, b[ un intervalle semi-ouvert à droite, f : [a, b[ ® R une fonction
continue. On dit que l"intégrale généralisée ∫[,[).(badxxf = ∫ b adxxf).( converge si ∫ c adxxf).( a une limite quand c ® b-0. Cette limite se note alors ∫[,[).(badxxf = limc®b-0 ∫ c adxxf).(.2) Soient I = ]a, b] un intervalle semi-ouvert à gauche, f : ]a, b] ® R une fonction continue. On dit
que l"intégrale généralisée ∫],]).(badxxf = ∫ b adxxf).( converge si ∫ b cdxxf).( a une limite quand c ® a+0. Cette limite se note alors ∫],]).(badxxf = limc®a+0 ∫ b cdxxf).(.3) Soient I = ]a, b[ un intervalle ouvert, f : ]a, b[ ® R une fonction continue. On dit que l"intégrale
généralisée ∫[,]).(badxxf = ∫ b adxxf).( converge si ∫ d cdxxf).( a une limite quand c ® a+0 et d ® b-0 indépendamment . Cette limite double se note alors ∫[,]).(badxxf = limc®a+0,d®b-0 ∫ d cdxxf).(. On dit que l"intégrale généralisée ∫Idxxf).( est divergente si ∫ c adxxf).(, resp.∫ b cdxxf).(, resp. d cdxxf).(, sont sans limite. On ne peut alors leur attribuer de valeur.Ces définitions s"étendent au cas où f est continue par morceaux sur tout segment [c, d] Ì I.
Remarque importante : Le symbole
∫Idxxf).( désigne deux objets bien distincts : l"intégralequotesdbs_dbs7.pdfusesText_13[PDF] appréciation 3eme trimestre primaire
[PDF] y=ax+b signification
[PDF] je cherche quelqu'un pour m'aider financièrement
[PDF] recherche aide a domicile personnes agées
[PDF] aide personne agée offre d'emploi
[PDF] tarif garde personne agée ? domicile
[PDF] y=ax+b graphique
[PDF] ménage chez personnes agées
[PDF] garde personne agee a son domicile
[PDF] cherche a garder personne agee a domicile
[PDF] calcul arithmétique de base
[PDF] ax2 bx c determiner a b et c
[PDF] opération arithmétique binaire
[PDF] rôle de la vitamine d dans l'organisme
