Primitives élémentaires Règles dintégration









FORMULAIRE d'INTÉGRATION Dans ce qui suit "c" est une

PRIMITIVES connues en terminale. ∫ a dx = ax + c. ∫ x dx = x2. 2 2+ kπ k ∈ Z ... ax + b. = 1 a ln
m


2.2 Quelques propriétés des intégrales définies

f(x)dx a et b sont les bornes d'intégration
amphi


Tableaux des dérivées

%20primitives


) Quelques formules de trigonométrie vraiment utiles. a





Analyse Numérique

d) Résoudre le système linéaire Ax = b en remplaçant PA par LU et en utilisant les algorithmes de substitution progressive et rétrograde. Exercice 2. 1) Pour 
Anum


Analyse Numérique

4.4 Analyse de l'erreur dans les méthodes d'intégration . . . . . . . . . . . . 79 Les bases b = 2 ou les puissances de 2 sont fréquemment utilisées par.
polyAnaNum


TD 1 Intégrales généralisées

16 sept. 2016 En somme quelles fonctions sont susceptibles d'intégration ? ... 2 l'intégrale d'une fonction continue. Pour calculer ∫b.
maths td support


Analyse numérique

Sortie : x = (xi)1≤i≤n ∈ Kn tel que Ax = b. 1. xn = bn ann. ;. 2. Pour i de n − 1 à 
PolyAnalyseNum





Calculs d'intégrales et de primitives

2. Intégration des fonctions rationnelles réelles. Fonctions rationnelles on isole c en multipliant par (x − 1) : (x − 1)F(x) = c + (x − 1)ax+b.
chap Primitives POLY


Primitives élémentaires Règles d'intégration

Règles d'intégration Soit une fonction f continue et positive sur [a;b]. ... Primitive. Intervalle f(x) = a. F(x) = ax. R f(x) = x. F(x) = x2. 2.
tableau primitives regles integration


L'usage de calculatrices est interdit.

Beaucoup de relations dépendent de x `a la fin des calculs. N'aboutit pas souvent mais souvent tenté. (b) Cette question est peu abordée. 2. (a) Cette question 
e a


212241 Primitives élémentaires Règles dintégration

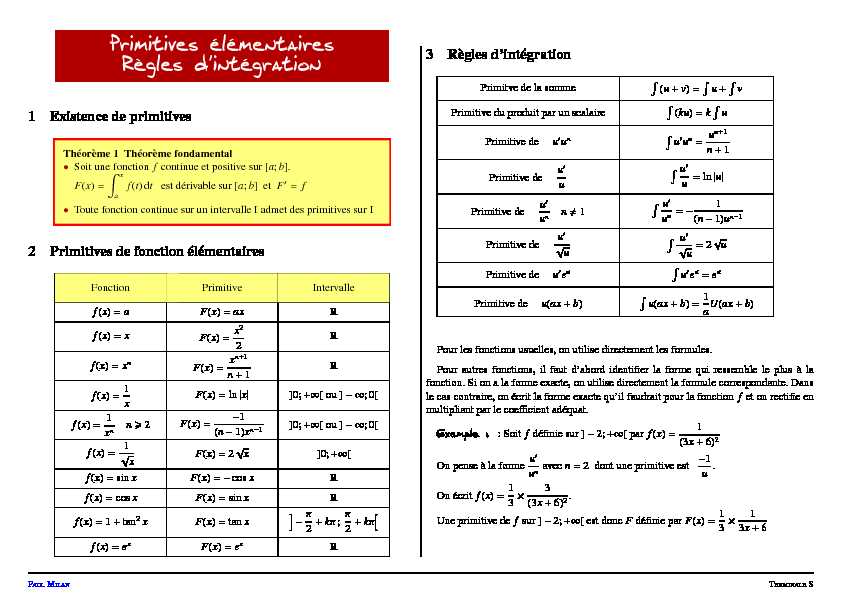
Primitives élémentaires

Règles d"intégration

1 Existence de primitives

Théorème 1 Théorème fondamental•Soit une fonctionfcontinue et positive sur [a;b].

F(x)=?

x a

f(t)dtest dérivable sur [a;b] etF?=f•Toute fonction continue sur un intervalle I admet des primitives sur I

2 Primitives de fonction élémentaires

Fonction

Primitive

Intervalle

f(x)=a

F(x)=ax

R f(x)=x

F(x)=x2

2 R f(x)=xn

F(x)=xn+1

n+1 R f(x)=1 x

F(x)=ln|x|

]0;+∞[ ou ]- ∞;0[ f(x)=1 xnn?2

F(x)=-1

(n-1)xn-1 ]0;+∞[ ou ]- ∞;0[ f(x)=1 ⎷x

F(x)=2⎷

x ]0;+∞[ f(x)=sinx

F(x)=-cosx

R f(x)=cosx

F(x)=sinx

R f(x)=1+tan2x

F(x)=tanx

2+kπ;π

2+kπ?

f(x)=ex

F(x)=ex

R

3 Règles d'intégration

Primitve de la somme

?(u+v)=?u+?v

Primitive du produit par un scalaire

?(ku)=k?u

Primitive deu?un

?u?un=un+1 n+1

Primitive deu?

u ?u? u=ln|u|

Primitive deu?

unn?1 ?u?un=-1 (n-1)un-1

Primitive deu?

⎷u ?u? ⎷u=2⎷ u

Primitive deu?eu

?u?eu=eu

Primitive deu(ax+b)

?u(ax+b)=1 aU(ax+b) Pour les fonctions usuelles, on utilise directement les formules. Pour autres fonctions, il faut d'abord identifier la forme qui ressemble leplus à la fonction. Si on a la forme exacte, on utilise directement la formule correspondante. Dans le cas contraire, on écrit la forme exacte qu'il faudrait pour la fonctionfet on rectifie en multipliant par le coefficient adéquat. Exemple :: Soitfdéfinie sur ]-2;+∞[ parf(x)=1 (3x+6)2

On pense à la forme

u? unavecn=2 dont une primitive est-1 u.

On écritf(x)=1

3×3

(3x+6)2. Une primitive defsur ]-2;+∞[ est doncFdéfinie parF(x)=1

3×1

3x+6

PaulMilan

TerminaleS

Primitives élémentaires

Règles d"intégration

1 Existence de primitives

Théorème 1 Théorème fondamental•Soit une fonctionfcontinue et positive sur [a;b].

F(x)=?

x a

f(t)dtest dérivable sur [a;b] etF?=f•Toute fonction continue sur un intervalle I admet des primitives sur I

2 Primitives de fonction élémentaires

Fonction

Primitive

Intervalle

f(x)=a

F(x)=ax

R f(x)=x

F(x)=x2

2 R f(x)=xn

F(x)=xn+1

n+1 R f(x)=1 x

F(x)=ln|x|

]0;+∞[ ou ]- ∞;0[ f(x)=1 xnn?2

F(x)=-1

(n-1)xn-1 ]0;+∞[ ou ]- ∞;0[ f(x)=1 ⎷x

F(x)=2⎷

x ]0;+∞[ f(x)=sinx

F(x)=-cosx

R f(x)=cosx

F(x)=sinx

R f(x)=1+tan2x

F(x)=tanx

2+kπ;π

2+kπ?

f(x)=ex

F(x)=ex

R

3 Règles d'intégration

Primitve de la somme

?(u+v)=?u+?v

Primitive du produit par un scalaire

?(ku)=k?u

Primitive deu?un

?u?un=un+1 n+1

Primitive deu?

u ?u? u=ln|u|

Primitive deu?

unn?1 ?u?un=-1 (n-1)un-1

Primitive deu?

⎷u ?u? ⎷u=2⎷ u

Primitive deu?eu

?u?eu=eu

Primitive deu(ax+b)

?u(ax+b)=1 aU(ax+b) Pour les fonctions usuelles, on utilise directement les formules. Pour autres fonctions, il faut d'abord identifier la forme qui ressemble leplus à la fonction. Si on a la forme exacte, on utilise directement la formule correspondante. Dans le cas contraire, on écrit la forme exacte qu'il faudrait pour la fonctionfet on rectifie en multipliant par le coefficient adéquat. Exemple :: Soitfdéfinie sur ]-2;+∞[ parf(x)=1 (3x+6)2

On pense à la forme

u? unavecn=2 dont une primitive est-1 u.

On écritf(x)=1

3×3

(3x+6)2. Une primitive defsur ]-2;+∞[ est doncFdéfinie parF(x)=1

3×1

3x+6

PaulMilan

TerminaleS


12345 Next